已知正数数列{an}的前n项和为Sn,满足an2=Sn+Sn-1(n≥2),a1=1.
(I)求证:数列{an}为等差数列,并求出通项公式;
(II)设bn=(1-an)2-a(1-an),若bn+1>bn对任意n∈N*恒成立,求实数a的取值范围.
解:(I)证明:∵a
n2=S
n+S
n-1(n≥2),∴

(n≥3).
两式相减可得a
n2 -
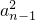
=S
n-s
n-2=a
n +a
n-1,∴a
n -a
n-1=1,
再由a
1=1,可得a
n=n.
(II)∵b
n=(1-a
n)
2-a(1-a
n),
∴b
n+1=
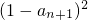
-a(1-a
n+1).
即b
n=(1-n)
2-a(1-n)=n
2+(a-2)n+1-a,b
n+1=[1-(n+1)]
2-a[1-(n+1)]=n
2+an.
故b
n+1-b
n=2n+a-1,
再由b
n+1>b
n对任意n∈N
*恒成立可得2n+a-1>0恒成立,故a>1-2n恒成立.
而1-2n的最大值为1-2=-1,故a>-1,
即实数a的取值范围(-1,+∞).
分析:(I)由 a
n2=S
n+S
n-1(n≥2),可得

(n≥3).两式相减可得 a
n -a
n-1=1,再由a
1=1,可得{a
n}的通项公式.
(II)根据{a
n}的通项公式化简b
n和b
n+1,由题意可得b
n+1-b
n=2n+a-1>0恒成立,故a>1-2n恒成立,而1-2n的最大值为-1,从而求得实数a的取值范围.
点评:本题主要考查等差关系的确定,等差数列的通项公式,函数的恒成立问题,属于难题.

 (n≥3).
(n≥3).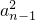 =Sn-sn-2=an +an-1,∴an -an-1=1,
=Sn-sn-2=an +an-1,∴an -an-1=1,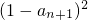 -a(1-an+1).
-a(1-an+1). (n≥3).两式相减可得 an -an-1=1,再由a1=1,可得{an}的通项公式.
(n≥3).两式相减可得 an -an-1=1,再由a1=1,可得{an}的通项公式.

 53天天练系列答案
53天天练系列答案