Question

10．如图，直三棱柱ABC-A₁B₁C₁，底面三角形ABC中，CA=CB=1，∠BCA=90°，棱AA₁=2，M、N分别为A₁B₁、AB的中点．
（1）求证：平面A₁NC∥平面BMC₁；（2）求异面直线A₁C与C₁N所成角的余弦值；
（3）求直线A₁N与平面ACC₁A₁所成角的正弦．

Answer 1

分析 （1）容易证明BM∥A₁N，C₁M∥CN，从而根据线面平行及面面平行的判定定理可得出平面A₁NC∥平面BMC₁；
（2）可分别以CA，CB，CC₁三直线为x，y，z轴，建立空间直角坐标系，从而可求出图形上一些点的坐标，从而得出向量$\overrightarrow{{A}_{1}C}，\overrightarrow{{C}_{1}N}$的坐标，根据cos$＜\overrightarrow{{A}_{1}C}，\overrightarrow{{C}_{1}N}＞$=$\frac{\overrightarrow{{A}_{1}C}•\overrightarrow{{C}_{1}N}}{|\overrightarrow{{A}_{1}C}||\overrightarrow{{C}_{1}N}|}$便可得出异面直线A₁C与C₁N所成角的余弦值；
（3）可以说明向量$\overrightarrow{BC}$为平面ACC₁A₁的一条法向量，设直线A₁N与平面ACC₁A₁所成角为θ，从而根据$sinθ=|cos＜\overrightarrow{{A}_{1}N}，\overrightarrow{BC}＞|$便可求出直线A₁N与平面ACC₁A₁所成角的正弦．

解答 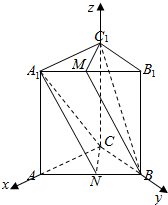解：（1）证明：根据条件知，四边形A₁NBM为平行四边形；
∴BM∥A₁N，A₁N?平面A₁NC，BM?平面A₁NC；
∴BM∥平面A₁NC；
连接MN，同理可证C₁M∥平面A₁NC；
又BM∩C₁M=M；
∴平面BMC₁∥平面A₁NC，即平面A₁NC∥平面BMC₁；
（2）根据条件可知CA，CB，CC₁三直线两两垂直，分别以这三直线为x，y，z轴，建立如图所示空间直角坐标系，则：
C（0，0，0），A（1，0，0），B（0，1，0），N（$\frac{1}{2}，\frac{1}{2}，0$），A₁（1，0，2），C₁（0，0，2）；
∴$\overrightarrow{{A}_{1}C}=（-1，0，-2），\overrightarrow{{C}_{1}N}=（\frac{1}{2}，\frac{1}{2}，-2）$；
∴$cos＜\overrightarrow{{A}_{1}C}，\overrightarrow{{C}_{1}N}＞=\frac{\overrightarrow{{A}_{1}C}•\overrightarrow{{C}_{1}N}}{|\overrightarrow{{A}_{1}C}||\overrightarrow{{C}_{1}N}|}$=$\frac{\frac{7}{2}}{\sqrt{5}•\sqrt{\frac{9}{2}}}=\frac{7\sqrt{10}}{30}$；
∴异面直线A₁C与C₁N所成角的余弦值为$\frac{7\sqrt{10}}{30}$；
（3）BC⊥AC，BC⊥CC₁，AC∩CC₁=C；
∴BC⊥平面ACC₁A₁；
∴$\overrightarrow{BC}=（0，-1，0）$为平面ACC₁A₁的一条法向量；
又$\overrightarrow{{A}_{1}N}=（-\frac{1}{2}，\frac{1}{2}，-2）$；
设直线A₁N与平面ACC₁A₁所成角为θ，则：
sinθ=$|cos＜\overrightarrow{{A}_{1}N}，\overrightarrow{BC}＞|$=$\frac{\frac{1}{2}}{\sqrt{\frac{9}{2}}}=\frac{\sqrt{2}}{6}$；
∴直线A₁N与平面ACC₁A₁所成角的正弦为$\frac{\sqrt{2}}{6}$．

点评 考查平行四边形的概念，线面平行和面面平行的判定定理，以及通过建立空间直角坐标系，利用空间向量解决异面直线所成角及线面角问题的方法，向量夹角余弦的坐标公式，平面法向量的概念，要清楚直线和平面所成角和直线的方向向量与平面法向量夹角的关系．