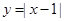练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若点(x, y)位于曲线与y＝2所围成的封闭区域, 则2x－y的最小值为       .
    .
    作出曲线与所表示的区域，令，即，作直线，在封闭区域内平行移动直线，当经过点时，取到最小值，此时最小值为．解题的关键在于画出曲线围成的封闭区域，并把求的最小值转化为求所表示的直线截距的最大值，通过平移直线即可求解．
    【考点定位】本题主要考查了线性规划的最值问题，考查画图和转化能力，属于中等题.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    已知函数的最小正周期为.
    （Ⅰ）求的值；
    （Ⅱ）求函数在区间上的值域.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    函数，，在上的部分图象如图所示，则的值为     ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列命题中正确的是 (    ）
    ①存在实数，使等式成立；②函数有无数个零点；③函数是偶函数；④方程的解集是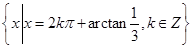；⑤把函数的图像沿轴方向向左平移个单位后，得到的函数解析式可以 表示成；⑥在同一坐标系中，函数的图像和函数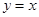的图像只有1个公共点．
    A．②③④ B．③⑤⑥C．①③⑤D．②③⑥

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    设函数.
    （Ⅰ）求的最小值，并求使取得最小值的的集合；
    （Ⅱ）不画图，说明函数的图像可由的图象经过怎样的变化得到.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知某海滨浴场的海浪高达y(米)是时间t(0≤t≤24，单位：小时)的函数，记作y＝f(t)．下表是某日各时的浪高数据.
    t(时)
    		0
    		3
    		6
    		9
    		12
    		15
    		18
    		21
    		24
    y(米)
    		1.5
    		1.0
    		0.5
    		1.0
    		1.5
    		1.0
    		0.5
    		0.99
    		1.5
    经长期观测，y＝f(t)的曲线可近似地看成是函数y＝Acosωt＋b.
    (1)根据以上数据，求出函数y＝Acosωt＋b的最小正周期T、振幅A及函数表达式；
    (2)依据规定，当海浪高度高于1米时才对冲浪爱好者开放，请依据(1)的结论，判断一天内的上午8：00至晚上20：00之间，有多长时间可供冲浪者进行运动？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    设函数f（x）＝sin（ωx＋），其中ω＞0，｜｜＜，若coscos－sinsin ＝0，且图象的一条对称轴离一个对称中心的最近距离是．
    （1）求函数f（x）的解析式；
    （2）若A,B,C是△ABC的三个内角，且f（A）＝－1，求sinB＋sinC的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    不查表求值： 

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知是第二象限角,，则     （　 　）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案