
11. 如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(![]() ,
,![]() ,0),点D在平面yOz内,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz内,且∠BDC=90°,∠DCB=30°.
(1)求![]() 的坐标;
的坐标;
(2)设![]() 和
和![]() 的夹角为
的夹角为![]() ,求cos
,求cos![]() 的值.
的值.
科目:高中数学 来源: 题型:
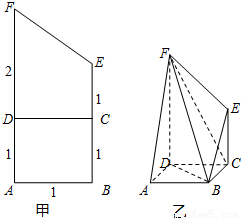
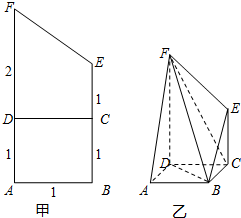 将(如图甲)直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图乙所示.
将(如图甲)直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图乙所示.查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 9 |
| y2 |
| 4 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市树德中学高三(上)12月段考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆市南开中学高二(下)期末数学试卷(文科)(解析版) 题型:解答题
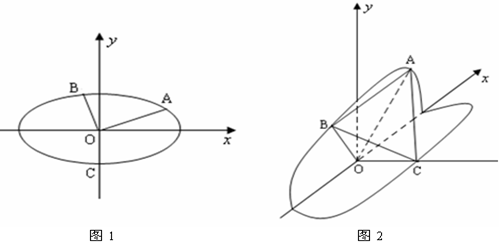
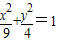 的下顶点为C,A,B分别在椭圆的第一象限和第二象限的弧上运动,满足
的下顶点为C,A,B分别在椭圆的第一象限和第二象限的弧上运动,满足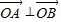 ,其中O为坐标原点,现沿x轴将坐标平面折成直二面角.如图2所示,在空间中,解答下列问题:
,其中O为坐标原点,现沿x轴将坐标平面折成直二面角.如图2所示,在空间中,解答下列问题: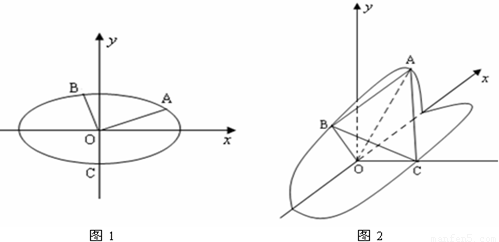
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com