
|
|
| n(1+2n-1) |
| 2 |


科目:高中数学 来源: 题型:
| t+2 |
| 2 |
| t2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:陕西省2009届高三教学质量检测模拟试题(一)、数学 题型:044
已知二次函数满足以下条件:
①图像关于直线x=![]() 对称;②f(1)=0;③其图像可由y=x2-1平移得到.
对称;②f(1)=0;③其图像可由y=x2-1平移得到.
(Ⅰ)求y=f(x)表达式;
(Ⅱ)若数列{an},{bn}对任意的实数x都满足f(x)·g(x)+anx+bn=xn+1(n∈N*),其中g(x)是定义在实数集R上的一个函数,求数列{an},{bn}的通项公式.
(Ⅲ)设圆Cn:(x-an)2+(y-bn)2=![]() ,(n∈N*),若圆Cn与圆Cn+1外切,且{rn}是各项都为正数的等比数列,求数列{rn}的公比q的值.
,(n∈N*),若圆Cn与圆Cn+1外切,且{rn}是各项都为正数的等比数列,求数列{rn}的公比q的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省杭州地区七校联考高三(上)期中数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:四川省雅安中学09-10学年高二上学期期中考试 题型:解答题
已知二次函数y=f(x)在x=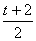 处取得最小值-
处取得最小值-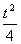 (t﹥0),f(1)=0, (1)求y=f(x)的表达式;(2)若任意实数x都满足等式f(x)g(x)+anx+bn=xn+1 (g(x)为多项式,n∈N+)试用t表示an和bn;(3)设圆Cn的方程为(x-an)2+(y-bn)2=r
(t﹥0),f(1)=0, (1)求y=f(x)的表达式;(2)若任意实数x都满足等式f(x)g(x)+anx+bn=xn+1 (g(x)为多项式,n∈N+)试用t表示an和bn;(3)设圆Cn的方程为(x-an)2+(y-bn)2=r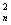 ,圆Cn与Cn+1
外切(n=1,2,3…),{rn}是各项都为正数的等比数列,记Sn为前n个圆的面积之和,求rn,sn。
,圆Cn与Cn+1
外切(n=1,2,3…),{rn}是各项都为正数的等比数列,记Sn为前n个圆的面积之和,求rn,sn。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com