
分析 游戏是否公平,关键要看游戏双方取胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
解答 解:设(x,y)表示小明抛掷骰子点数是x,小刚抛掷骰子点数是y,则该概率属于古典概型.
所有的基本事件是:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),
即有36种基本事件. …(2分)
其中点数之和为奇数的基本事件有:(1,2),(1,4),(1,6),(2,1),(2,3),(2,5),(3,2),(3,4),(3,6),
(4,1),(4,3),(4,5),(5,2),(5,4),(5,6),(6,1),(6,3),(6,5).
即有18种.…(2分)
所以小刚得(1分)的概率是$\frac{18}{36}$=$\frac{1}{2}$…(2分)
则小明得(1分)的概率是1-$\frac{1}{2}=\frac{1}{2}$…(2分)
则小明获胜的概率与小刚获胜的概率相同,游戏公平…(2分)
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (1,2) | C. | (1,-2) | D. | (-1,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
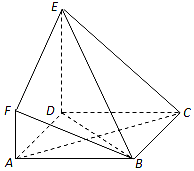 如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角为45°.
如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角为45°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6,9,15 | B. | 3,9,18 | C. | 3,6,11 | D. | 3,8,19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 3 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com