
【题目】已知圆C:x2+y2+2x﹣3=0.
(1)求圆的圆心C的坐标和半径长;
(2)直线l经过坐标原点且不与y轴重合,l与圆C相交于A(x1 , y1)、B(x2 , y2)两点,求证: ![]() 为定值;
为定值;
(3)斜率为1的直线m与圆C相交于D、E两点,求直线m的方程,使△CDE的面积最大.
【答案】
(1)解:圆C:x2+y2+2x﹣3=0,配方得(x+1)2+y2=4,
则圆心C的坐标为(﹣1,0),圆的半径长为2
(2)解:设直线l的方程为y=kx,
联立方程组 ![]() ,
,
消去y得(1+k2)x2+2x﹣3=0,
则有: ![]() ;
;
所以 ![]() 为定值
为定值
(3)解:解法一:设直线m的方程为y=kx+b,则圆心C到直线m的距离 ![]() ,
,
所以 ![]() ,
,
![]() ≤
≤ ![]() ,
,
当且仅当 ![]() ,即
,即 ![]() 时,△CDE的面积最大,
时,△CDE的面积最大,
从而 ![]() ,解之得b=3或b=﹣1,
,解之得b=3或b=﹣1,
故所求直线方程为x﹣y+3=0或x﹣y﹣1=0.
解法二:由(1)知|CD|=|CE|=R=2,
所以 ![]() ≤2,
≤2,
当且仅当CD⊥CE时,△CDE的面积最大,此时 ![]() ;
;
设直线m的方程为y=x+b,则圆心C到直线m的距离 ![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
由 ![]() ,得b=3或b=﹣1,
,得b=3或b=﹣1,
故所求直线方程为x﹣y+3=0或x﹣y﹣1=0
【解析】(1)把圆C的方程化为标准方程,写出圆心和半径;(2)设出直线l的方程,与圆C的方程组成方程组,消去y得关于x的一元二次方程,由根与系数的关系求出 ![]() 的值;(3)解法一:设出直线m的方程,由圆心C到直线m的距离,写出△CDE的面积,利用基本不等式求出最大值,从而求出对应直线方程;解法二:利用几何法得出CD⊥CE时△CDE的面积最大,再利用点到直线的距离求出对应直线m的方程.
的值;(3)解法一:设出直线m的方程,由圆心C到直线m的距离,写出△CDE的面积,利用基本不等式求出最大值,从而求出对应直线方程;解法二:利用几何法得出CD⊥CE时△CDE的面积最大,再利用点到直线的距离求出对应直线m的方程.


科目:高中数学 来源: 题型:
【题目】已知数列{an}是公比不为1的等比数列,a1=1,且a1 , a3 , a2成等差数列.
(1)求数列{an}的通项;
(2)若数列{an}的前n项和为Sn , 试求Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60° 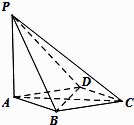
(1)若PA=AB,求PB与平面PDC所成角的正弦值;
(2)当平面PBC与平面PDC垂直时,求PA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为π,若其图象向左平移
)的最小正周期为π,若其图象向左平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点( ![]() ,0)对称
,0)对称
B.关于点(﹣ ![]() ,0)对称
,0)对称
C.关于直线x=﹣ ![]() 对称
对称
D.关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形, 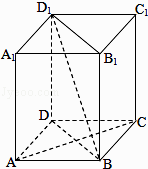
(1)若E为DD1的中点,证明:BD1∥面EAC
(2)求证:AC⊥平面BB1D1D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2, ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinB=2sinA,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A>0,ω>0,﹣ ![]() <φ<
<φ< ![]() ,x∈R)的部分图象如图所示.
,x∈R)的部分图象如图所示. 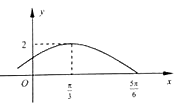
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)将函数y=f(x)的图象沿x轴方向向右平移 ![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的 ![]() (纵坐标不变),得到函数y=g(x)的图象,当x∈[﹣
(纵坐标不变),得到函数y=g(x)的图象,当x∈[﹣ ![]() ,
, ![]() ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2, 3x4﹣2,3x5﹣2的平均数和方差分别是 .
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2, 3x4﹣2,3x5﹣2的平均数和方差分别是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x的图象与函数y=g(x)的图象关于直线y=x对称,令h(x)=g(1﹣x2),则关于函数y=h(x)的下列4个结论: ①函数y=h(x)的图象关于原点对称;
)x的图象与函数y=g(x)的图象关于直线y=x对称,令h(x)=g(1﹣x2),则关于函数y=h(x)的下列4个结论: ①函数y=h(x)的图象关于原点对称;
②函数y=h(x)为偶函数;
③函数y=h(x)的最小值为0;
④函数y=h(x)在(0,1)上为增函数
其中,正确结论的序号为 . (将你认为正确结论的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com