
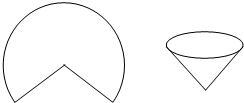
 如图,用半径为10
如图,用半径为10| 2 |
| 2 |
| 2 |
| 2 |
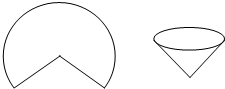 解:设铁皮扇形的半径和弧长分别为R、l,圆锥形容器的高和底面半径分别为h、r,
解:设铁皮扇形的半径和弧长分别为R、l,圆锥形容器的高和底面半径分别为h、r,| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
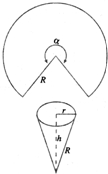 如图,用半径为R的圆铁皮,剪一个圆心角为α的扇形,制成一个圆锥形的漏斗,问圆心角α取什么值时,漏斗容积最大.(圆锥体积公式:V=
如图,用半径为R的圆铁皮,剪一个圆心角为α的扇形,制成一个圆锥形的漏斗,问圆心角α取什么值时,漏斗容积最大.(圆锥体积公式:V=| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:2011届上海市静安区高三下学期质量调研考试数学理卷 题型:单选题
如图,用半径为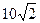 cm,面积为
cm,面积为
 cm2的扇形铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计), 该容器最多盛水多少?(结果精确到0.1 cm3)
cm2的扇形铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计), 该容器最多盛水多少?(结果精确到0.1 cm3)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市静安区高三下学期质量调研考试数学理卷 题型:选择题
如图,用半径为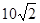 cm,面积为
cm,面积为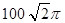 cm2的扇形铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计),
该容器最多盛水多少?(结果精确到0.1 cm3)
cm2的扇形铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计),
该容器最多盛水多少?(结果精确到0.1 cm3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com