
 ,直线l与椭圆C相交于A、B两点,
,直线l与椭圆C相交于A、B两点, (其中O为坐标原点).
(其中O为坐标原点). ;当直线AB的斜率存在时,设直线AB的方程为y=kx+m,与椭圆C:
;当直线AB的斜率存在时,设直线AB的方程为y=kx+m,与椭圆C: 联立,得:(1+4k2)x2+8kmx+4m2-4=0,由根与系数的关系得到O到直线AB的距离d=
联立,得:(1+4k2)x2+8kmx+4m2-4=0,由根与系数的关系得到O到直线AB的距离d= =
= .由此能求出点O到直线AB的距离为定值
.由此能求出点O到直线AB的距离为定值 .
. ,解方程组
,解方程组 ,得
,得 ,同理可求得
,同理可求得 ,由此能推导出|OA|•|OB|的最小值.
,由此能推导出|OA|•|OB|的最小值. .在Rt△OAB中,d=
.在Rt△OAB中,d= ,故有
,故有 =
= ,由此能求出|OA|•|OB|的最小值.
,由此能求出|OA|•|OB|的最小值. .设∠OAH=θ,则∠BOH=θ,故|OA|=
.设∠OAH=θ,则∠BOH=θ,故|OA|= ,|OB|=
,|OB|= .所以,|OA|×|OB|=
.所以,|OA|×|OB|= =
= ,由此能求出|OA|•|OB|的最小值.
,由此能求出|OA|•|OB|的最小值. ,即x1x2+y1y2=0,也就是
,即x1x2+y1y2=0,也就是 ,代入椭圆方程解得:
,代入椭圆方程解得: .
. .…(2分)
.…(2分) 联立,
联立, ,
, ,…(3分)
,…(3分) ,…(4分)
,…(4分) ,
, =
= .
. .…(6分)
.…(6分) ,
, ,得
,得 ,
, ,
,
 .…(9分)
.…(9分) =4
=4 ,
, =-9
=-9 (t>1),所以4<g(t)≤
(t>1),所以4<g(t)≤ ,即
,即 .…(11分)
.…(11分) ,故|OA|•|OB|的最小值为
,故|OA|•|OB|的最小值为 ,最大值为2.…(13分)
,最大值为2.…(13分) .
. ,故有
,故有 =
= ,
, ,…(9分)
,…(9分)

 ,
, ,(当且仅当|OA|=|OB|时取等号).…(11分)
,(当且仅当|OA|=|OB|时取等号).…(11分) .…(13分)
.…(13分) .
. ,|OB|=
,|OB|= .…(9分)
.…(9分) =
= ,…(11分)
,…(11分) ,即
,即 时,|OA|•|OB|取得最小值,最小值为
时,|OA|•|OB|取得最小值,最小值为 .…(13分)
.…(13分)

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源: 题型:解答题
 ,直线l:y=ax+b(a,b∈R)
,直线l:y=ax+b(a,b∈R)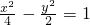 ,或改为抛物线方程y2=4x,再在第(4)问添加的条件中选择一个,求出直线l的方程.
,或改为抛物线方程y2=4x,再在第(4)问添加的条件中选择一个,求出直线l的方程.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
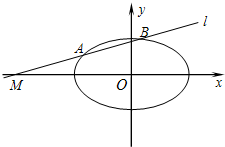 已知椭圆C:
已知椭圆C: ,直线l过点M(m,0).
,直线l过点M(m,0).查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省嘉兴市海宁市高三(下)期初数学试卷(理科)(解析版) 题型:解答题
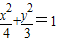 ,直线l过点M(m,0).
,直线l过点M(m,0).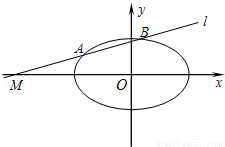
查看答案和解析>>
科目:高中数学 来源:2010年东北育才、大连育明高三第二次联考数学试卷(理科)(解析版) 题型:选择题
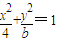 ,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com