设一个正三棱锥的侧面与底面所成的角为α,相邻两个侧面所成的角为β,那么两个角α和β的三角函数间的关系是( )
A.2cos2α+3cosβ=1
B.2cosα+3cos2β=1
C.3cos2α+2cosβ=1
D.3cosα+2cos2β=1
【答案】
分析:由题设条件及四个选项可以得出需要先做出两个二面角,再由题设中的等量关系建立方程研究两个二面角的关系,由图形及题设条件知在如图图形中作SD⊥BC,连接AD,作SH⊥AD,则SH⊥底面ABC,可得BE⊥SA,连接CE,则CE⊥SA,∠BEC是二侧面成角的平面角,观察三角形BEC,可将此三角形的边用要研究的角α,β表示出来,在此三角形中利用余弦定理得到方程,整理出选项.
解答:解:
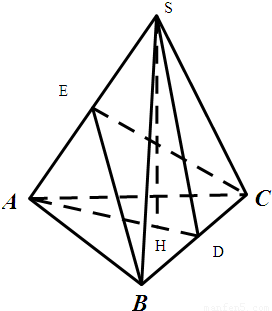
设正三棱锥S-ABC,侧面与底面所成的角为α,相邻两个侧面所成的角为β,作SD⊥BC,连接AD,作SH⊥AD,则SH⊥底面ABC,可得BE⊥SA,连接CE,则CE⊥SA,∠BEC是二侧面成角的平面角,
设AB=BC=AC=1个单位,
AD=
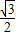
,HD=
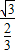
=
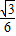
,AH=
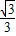
,
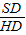
=cosα,SD=
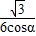
,SH=
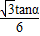
,
SA=
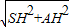
=
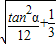
=
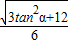
,
又BE×SA×

=SD×AB×

=S
△SAB,
∴BE=
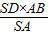
=
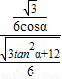
=

在三角形EBC中根据余弦定理,
BC
2=BE
2+EC
2-2×BE×EC×cosβ,
1=
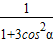
+
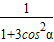
-2×
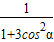
×cosβ,
经整理得:3cos
2α+2cosβ=1,
故选C
点评:本题考查二面角的平面角及求法,由于本题是要研究两个二面角有关的方程问题,从题设条件中找到等量关系是解题的关键,本题中用余弦定理建立起等式,整理出答案,本题中熟练掌握二面角平面角的作法也很关键,本题考查了推理论证能力及空间想像感知能力,且与余弦定理想结合,综合性较强,有一定的思维深度,运算量较大易因为计算出错或因为找不到等量关系而卖到解题无法下手.

 设正三棱锥S-ABC,侧面与底面所成的角为α,相邻两个侧面所成的角为β,作SD⊥BC,连接AD,作SH⊥AD,则SH⊥底面ABC,可得BE⊥SA,连接CE,则CE⊥SA,∠BEC是二侧面成角的平面角,
设正三棱锥S-ABC,侧面与底面所成的角为α,相邻两个侧面所成的角为β,作SD⊥BC,连接AD,作SH⊥AD,则SH⊥底面ABC,可得BE⊥SA,连接CE,则CE⊥SA,∠BEC是二侧面成角的平面角,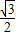 ,HD=
,HD=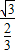 =
=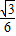 ,AH=
,AH=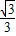 ,
,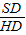 =cosα,SD=
=cosα,SD=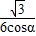 ,SH=
,SH=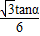 ,
,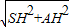 =
=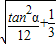 =
=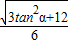 ,
, =SD×AB×
=SD×AB× =S△SAB,
=S△SAB,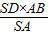 =
=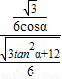 =
=
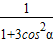 +
+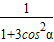 -2×
-2×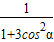 ×cosβ,
×cosβ,
