
【题目】如图,已知矩形ABCD,![]() ,
,![]() ,AF⊥平面ABC,且
,AF⊥平面ABC,且![]() .E为线段DC上一点,沿直线AE将△ADE翻折成
.E为线段DC上一点,沿直线AE将△ADE翻折成![]() ,M为
,M为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 体积的最小值是________.
体积的最小值是________.
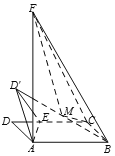
【答案】![]()
【解析】
首先分析出![]() ,即求棱锥
,即求棱锥![]() 体积的最小值即求点
体积的最小值即求点![]() 到平面
到平面![]() 的距离的最小值,转化为求点
的距离的最小值,转化为求点![]() 到平面
到平面![]() 距离的最小值,由条件确定点
距离的最小值,由条件确定点![]() 的运动轨迹为以
的运动轨迹为以![]() 为球心,半径为1的球面的一部分,然后根据图象分析点
为球心,半径为1的球面的一部分,然后根据图象分析点![]() 到平面
到平面![]() 距离的最小值.
距离的最小值.
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]()
![]() ,
,
所以![]() ,
,
所以求棱锥![]() 体积的最小值即求点
体积的最小值即求点![]() 到平面
到平面![]() 的距离的最小值,
的距离的最小值,
因为点![]() 是
是![]() 的中点,
的中点,
所以点![]() 到平面
到平面![]() 的距离是点
的距离是点![]() 到平面
到平面![]() 距离的一半,
距离的一半,
因为![]() ,随着点
,随着点![]() 在线段
在线段![]() 上移动,
上移动,
点![]() 的运动轨迹为以
的运动轨迹为以![]() 为球心,半径为1的球面的一部分,
为球心,半径为1的球面的一部分,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,并且交于
,并且交于![]() ,
,
所以如图,过点![]() 作
作![]() ,即
,即![]() 平面
平面![]() ,
,
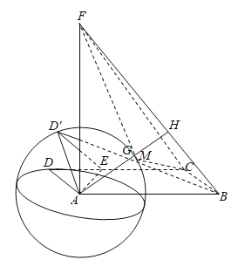
当![]() 为
为![]() 与球面的交点
与球面的交点![]() 时,
时,![]() 到平面
到平面![]() 的距离最小,
的距离最小,
此时点![]() 在线段
在线段![]() 上,
上,
根据![]() ,
,
可得![]() ,此时
,此时![]() ,
,
即![]() 到平面
到平面![]() 的距离的最小值是
的距离的最小值是![]() ,那么点
,那么点![]() 到平面
到平面![]() 距离的最小值是
距离的最小值是![]() ,
,
所以三棱锥![]() 体积的最小值是
体积的最小值是![]() .
.
故答案为:![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,椭圆C截直线y=1所得线段的长度为
,椭圆C截直线y=1所得线段的长度为![]() .
.
(Ⅰ)求椭圆C的方程;
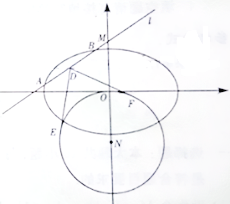
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|. 设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求![]() EDF的最小值.
EDF的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在圆心角为直角,半径为![]() 的扇形区域内进行野外生存训练.如图所示,在相距
的扇形区域内进行野外生存训练.如图所示,在相距![]() 的
的![]() ,
,![]() 两个位置分别为300,100名学生,在道路
两个位置分别为300,100名学生,在道路![]() 上设置集合地点
上设置集合地点![]() ,要求所有学生沿最短路径到
,要求所有学生沿最短路径到![]() 点集合,记所有学生进行的总路程为
点集合,记所有学生进行的总路程为![]() .
.
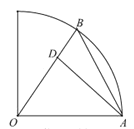
(1)设![]() ,写出
,写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当![]() 最小时,集合地点
最小时,集合地点![]() 离点
离点![]() 多远?
多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有下界,其中
上有下界,其中![]() 为函数
为函数![]() 的一个下界;若存在
的一个下界;若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有上界,其中
上有上界,其中![]() 为函数
为函数![]() 的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.
的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.
下述四个结论:①1不是函数![]() 的一个下界;②函数
的一个下界;②函数![]() 有下界,无上界;③函数
有下界,无上界;③函数![]() 有上界,无下界;④函数
有上界,无下界;④函数![]() 有界.
有界.
其中所有正确结论的编号是( )
A.①②B.②④C.③④D.②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 恒成立?请说明理由.
恒成立?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥M-ABCD中,MB⊥平面ABCD,四边形ABCD是矩形,AB=MB,E、F分别为MA、MC的中点.
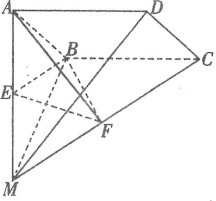
(1)求证:平面BEF⊥平面MAD;
(2)若![]() ,求三棱锥E-ABF的体积.
,求三棱锥E-ABF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线与x轴的交点为H,点F为抛物线的焦点,点P在抛物线上且
的准线与x轴的交点为H,点F为抛物线的焦点,点P在抛物线上且![]() ,当k最大时,点P恰好在以H,F为焦点的双曲线上,则k的最大值为_____,此时该双曲线的离心率为_____.
,当k最大时,点P恰好在以H,F为焦点的双曲线上,则k的最大值为_____,此时该双曲线的离心率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com