
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
分析 由导数性质推导出当x∈(-∞,0)或x∈(0,+∞)时,函数y=xf(x)单调递减.由此能求出结果.
解答 解:∵函数y=f(x-1)的图象关于直线x=1对称,
∴y=f(x)关于y轴对称,
∴函数y=xf(x)为奇函数.
∵[xf(x)]'=f(x)+xf'(x),
∴当x∈(-∞,0)时,[xf(x)]'=f(x)+xf'(x)<0,函数y=xf(x)单调递减,
当x∈(0,+∞)时,函数y=xf(x)单调递减.
∵$0<sin\frac{1}{2}<\frac{1}{2}$,$1>ln2>ln\sqrt{e}=\frac{1}{2}$,${log_{\frac{1}{2}}}\frac{1}{4}=2$,$0<sin\frac{1}{2}<ln2<{log_{\frac{1}{2}}}\frac{1}{4}$,
∴a>b>c.
故选:A.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意导数性质、函数性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,圆柱内有一个直三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形.如果三棱柱的体积为$12\sqrt{3}$,圆柱的底面直径与母线长相等,则圆柱的侧面积为( )
如图,圆柱内有一个直三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形.如果三棱柱的体积为$12\sqrt{3}$,圆柱的底面直径与母线长相等,则圆柱的侧面积为( )| A. | 12π | B. | 14π | C. | 16π | D. | 18π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
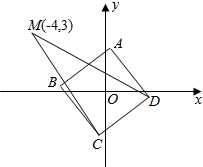 如图所示,ABCD是以原点O为中心、边长为2的正方形,M点坐标为(-4,3),当正方形在满足上述条件下转动时,$\overrightarrow{MC}•\overrightarrow{MD}$的取值范围是[15,35].
如图所示,ABCD是以原点O为中心、边长为2的正方形,M点坐标为(-4,3),当正方形在满足上述条件下转动时,$\overrightarrow{MC}•\overrightarrow{MD}$的取值范围是[15,35].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
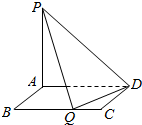 如图所示,矩形ABCD的边AB=m,BC=4,PA⊥平面ABCD,PA=3,现有数据:
如图所示,矩形ABCD的边AB=m,BC=4,PA⊥平面ABCD,PA=3,现有数据:| A. | ①② | B. | ①②③ | C. | ②④ | D. | ① |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com