
(本小题共10分)
已知函数
(1)解关于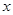 的不等式
的不等式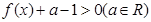 ;
;
(2)若函数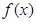 的图象恒在函数
的图象恒在函数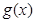 图象的上方(没有公共点),求
图象的上方(没有公共点),求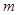 的取值范围。
的取值范围。
(1)当a=1时,解集为(-∞,2)∪(2,+∞);当a>1时,解集为R,当a<1时,解集为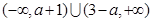 ;(2)
;(2)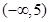
【解析】
试题分析:(Ⅰ)不等式f(x)+a-1>0即为|x-2|+a-1>0,
当a=1时,解集为x≠2,即(-∞,2)∪(2,+∞);
当a>1时,解集为全体实数R;
当a<1时,解集为(-∞,a+1)∪(3-a,+∞).
(Ⅱ)f(x)的图象恒在函数g(x)图象的上方,即为|x-2|>-|x+3|+m对任意实数x恒成立,即|x-2|+|x+3|>m恒成立,(7分)
又由不等式的性质,对任意实数x恒有|x-2|+|x+3|≥|(x-2)-(x+3)|=5,于是得m<5,
故m的取值范围是(-∞,5).
考点:本题考查了绝对值不等式的解法及恒成立问题
点评:在解答含有绝对值不等式问题时,要注意分段讨论来取绝对值符号的及利用绝对值的几何意义来求含有多个绝对值的最值问题


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源:2010-2011年广东省龙川一中高一第二学期入学考试数学试卷 题型:解答题
(本小题共10分)
三棱柱ABC—A1B1C1中,CC1⊥平面ABC,△ABC是边长为2的等边三角形,D为AB边中点,且CC1=2AB.
(1)(4′)求证:平面C1CD⊥平面ABC;
(2)(6′)求三棱锥D—CBB1的体积.
查看答案和解析>>
科目:高中数学 来源:2014届河北省高一下学期期末数学试卷(解析版) 题型:解答题
(本小题共10分)
已知 的三个角
的三个角 的对边分别为
的对边分别为 ,且
,且 成等差数列,且
成等差数列,且 。数列
。数列 是等比数列,且首项
是等比数列,且首项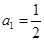 ,公比为
,公比为 。
。
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 。
。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广西省南宁市高三第二次适应性考试数学理卷 题型:解答题
(本小题共10分)(注意:在试题卷上作答无效)
斜三角形ABC的面积为S,且 ,且
,且 ,求
,求
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三上学期入学考试理科数学卷 题型:解答题
(本小题共10分) 已知集合A= ,
, B=
B= ,C=
,C=
①求A∩B;
②若(A∩B) C,求m的取值范围。
C,求m的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年内蒙古包头市高三上学期期中考试数学试卷 题型:解答题
(本小题共10分)
已知 为等差数列,且
为等差数列,且 ,
, 。
。
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若等比数列 满足
满足 ,
, ,求
,求 的前n项和公式
的前n项和公式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com