(I)∵数列{b
n}是公比为β的等比数列,∴b
n=βb
n-1,∴a
n+1-αa
n=β(a
n-a
n-1)…(2分)
即a
n+1=(α+β)a
n-αβa
n-1,又
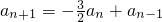
,
∴
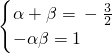
…(4分)∴α,β是方
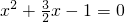
的两根,
∴
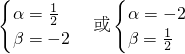
…(6分)
(II)假设存在正整数k,n使得ka
n+2+a
n与ka
n+3+a
n+1有大于1的公约数d,
d也是(ka
n+3+a
n+1)-(ka
n+2+a
n)即k(a
n+3-a
n+2)+k(a
n+1-a
n)的约数,
依题设a
n+3-a
n+2=a
n+1,a
n+1-a
n=a
n-1,
∴d是ka
n+1+a
n-1的约数…(8分)
从而d是ka
n+2+a
n与ka
n+1+a
n-1的公约数
同理可得d是ka
n+a
n-2的约数依此类推,d是ka
4+a
2与ka
3+a
1的约数…(10分)
又a
1=1,a
2=1,故a
3=2,a
4=3,
于是ka
4+a
2=3k+1,ka
3+a
1=2k+1 …(12分)
又∵(3k+1)-(2k+1)=k,∴d是k的约数和2k+1的约数,
∴d是(2k+1)-k即k+1的约数
从而d是(k+1)-k即1的约数,这与d>1矛盾
故不存在k,n是ka
n+2+a
n与ka
n+3+a
n+1有大于1的公约数.
分析:(I)根据a
n+1=λa
n+a
n-1,

,数列b
n是公比为β的等比数列,
可求得a
n+1=(α+β)a
n-αβa
n-1,又
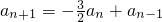
,从而可求得α,β的值;
(II)可假设存在正整数k,n使得ka
n+2+a
n与ka
n+3+a
n+1有大于1的公约数d,d也是(ka
n+3+a
n+1)-(ka
n+2+a
n)即k(a
n+3-a
n+2)+k(a
n+1-a
n)的约数,从而推出d是ka
n+1+a
n-1的约数,也是ka
n+2+a
n与ka
n+1+a
n-1的公约数;依此类推,d是ka
4+a
2与ka
3+a
1的约数;最终导出d是(k+1)-k即1的约数,这与d>1矛盾,从而结论.
点评:本题考查等比数列的性质,着重考查学生综合分析与应用公示的能力,推理论证的能力,属于难题.

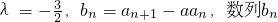 是公比为β的等比数列,求α和β的值.
是公比为β的等比数列,求α和β的值.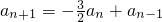 ,
,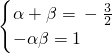 …(4分)∴α,β是方
…(4分)∴α,β是方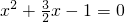 的两根,
的两根,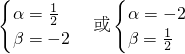 …(6分)
…(6分) ,数列bn是公比为β的等比数列,
,数列bn是公比为β的等比数列,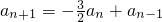 ,从而可求得α,β的值;
,从而可求得α,β的值;

 同步练习强化拓展系列答案
同步练习强化拓展系列答案 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.