
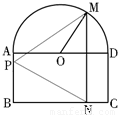
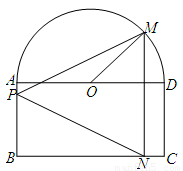
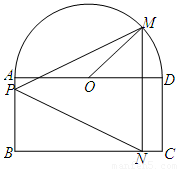
 如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪出一个等腰三角形PMN,其底边MN⊥BC.
如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪出一个等腰三角形PMN,其底边MN⊥BC. MN•AQ可求
MN•AQ可求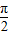 ],结合锐角三角函数的定义可求MQ=sinθ,OQ=cosθ,代入三角形的面积公式S△PMN=
],结合锐角三角函数的定义可求MQ=sinθ,OQ=cosθ,代入三角形的面积公式S△PMN= MN•AQ=
MN•AQ= (1+sinθ)(1+cosθ)展开利用换元法,转化为二次函数的最值求解
(1+sinθ)(1+cosθ)展开利用换元法,转化为二次函数的最值求解 ,OQ=
,OQ=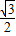 (算出一个得2分)
(算出一个得2分) MN•AQ=
MN•AQ= ×
× ×(1+
×(1+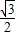 )=
)=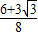 …(6分)
…(6分)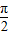 ],MQ=sinθ,OQ=cosθ
],MQ=sinθ,OQ=cosθ MN•AQ=
MN•AQ= (1+sinθ)(1+cosθ)
(1+sinθ)(1+cosθ) (1+sinθcosθ+sinθ+cosθ)….(11分)
(1+sinθcosθ+sinθ+cosθ)….(11分)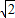 ],
], (t+1+
(t+1+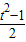 )
)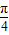 ,当t=
,当t=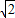 ,
,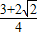 .…..…(14分)
.…..…(14分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
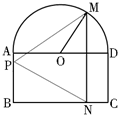 如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪出一个等腰三角形PMN,其底边MN⊥BC.
如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪出一个等腰三角形PMN,其底边MN⊥BC.查看答案和解析>>
科目:高中数学 来源:2014届湖北省高三10月统一阶段性考试理科数学试卷(解析版) 题型:解答题
如图所示,一个半圆和长方形组成的铁皮,长方形的边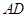 为半圆的直径,
为半圆的直径,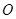 为半圆的圆心,
为半圆的圆心,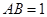 ,
,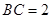 ,现要将此铁皮剪出一个等腰三角形
,现要将此铁皮剪出一个等腰三角形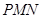 ,其底边
,其底边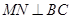 .
.
(1)设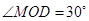 ,求三角形铁皮
,求三角形铁皮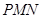 的面积;
的面积;
(2)求剪下的铁皮三角形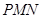 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2014届湖北省高三10月统一阶段性考试文科数学试卷(解析版) 题型:解答题
如图所示,一个半圆和长方形组成的铁皮,长方形的边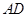 为半圆的直径,
为半圆的直径,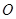 为半圆的圆心,
为半圆的圆心,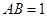 ,
,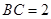 ,现要将此铁皮剪出一个等腰三角形
,现要将此铁皮剪出一个等腰三角形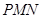 ,其底边
,其底边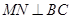 .
.
(1)设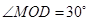 ,求三角形铁皮
,求三角形铁皮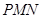 的面积;
的面积;
(2)求剪下的铁皮三角形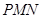 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,一个半圆和长方形组成的铁皮,长方形的边![]() 为半圆的直径,
为半圆的直径,![]() 为半圆的圆心,
为半圆的圆心,![]() ,
,![]() ,现要将此铁皮剪出一个等腰三角形
,现要将此铁皮剪出一个等腰三角形![]() ,其底边
,其底边![]() .
.
(1)设![]() ,求三角形铁皮
,求三角形铁皮![]() 的面积;
的面积;
(2)求剪下的铁皮三角形![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com