解:设圆的方程为:(x-a)
2+(y-b)
2=r
2∵直线2x+y=0平分圆,
则:圆心在直线2x+y=0上,则2a+b=0?b=-2a(2分)
又直线x-y+1=0与圆相交所得的弦长为

,
由圆的几何性质可得:圆心到该直线的距离为

(2分)
即:
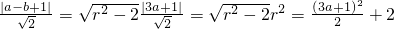
(2分)
∴该圆的方程为
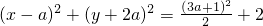
,
把A的坐标(2,3)代入圆的方程得:a
2+10a+21=0,
解得:a=-3或a=-7,
∴圆的方程为:(x+3)
2+(y-6)
2=34或(x+7)
2+(y-14)
2=202.
分析:由圆心为(a,b),半径为r,设出圆的标准方程,由直线2x+y=0平分圆C得到圆心C在直线上,把圆心的坐标代入已知直线方程用a表示出b,然后根据圆C与直线x-y+1=0相交的弦长,根据垂径定理及勾股定理,由圆的半径r及弦长的一半表示出圆心到直线x-y+1=0的距离,利用点到直线的距离公式,表示出圆心到直线x-y+1=0的距离,两者相等,用a表示出r,将表示出的b和半径r代入圆的方程消去b和r,再把A的坐标代入圆的方程,即可求出a的值,从而确定出圆的方程.
点评:此题考查了直线与圆相交的性质,垂径定理、勾股定理及圆的对称性,点到直线的距离公式,要求学生综合圆的几何性质来解决问题,解答此类题常常利用待定系数法来求出圆的标准方程,同时在解答时注意消去参数b和r.

 ,求圆C的方程.
,求圆C的方程. ,
, (2分)
(2分)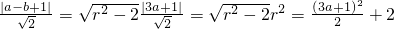 (2分)
(2分)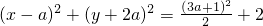 ,
,

 阅读快车系列答案
阅读快车系列答案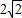 ,求圆C的方程.
,求圆C的方程.