练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    奇函数f(x)＝ax3＋bx2＋cx在x＝处有极值，则ac＋2b的值为

    [　　]

    A．3

    B．－3

    C．0

    D．1

    答案：B
    解析：

    　　∵(x)＝3ax2＋2bx＋c，

    　　∴()＝0．

    　　∴3a·＋2b·＋c＝0．

    　　∴3＋2b＋ac＝0．

    　　∴ac＋2b＝－3．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：山东省济宁一中2011届高三上学期第一次月考数学理科试题 题型：044

    已知函数f(x)＝ax＋＋c(a，b，c是常数)是奇函数且满足f(1)＝，f(2)＝．

    (Ⅰ)求a、b、c的值；

    (Ⅱ)是判断函数f(x)在(0，)上的单调性并说明理由；

    (Ⅲ)试求函数f(x)在(0，＋∞)上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分12分）已知函数f(x)＝ax＋(x≠0，常数a∈R).

    (1)讨论函数f(x)的奇偶性，并说明理由；

    (2)若函数f(x)在x∈[3，＋∞)上为增函数，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年安徽省合肥市高三第一次月考文科数学试卷 题型：解答题

    (13分)已知函数f(x)＝ax＋(x≠0，常数a∈R).

     

    (1)讨论函数f(x)的奇偶性，并说明理由；

    (2)若函数f(x)在x∈[3，＋∞)上为增函数，求a的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2014届陕西省高一上学期期末考试数学 题型：解答题

    （13分）已知函数f(x)＝ax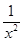＋ (x≠0，常数a∈R)．

    (1)讨论函数f(x)的奇偶性，并说明理由；

    (2)若函数f(x)在x∈[3，＋∞)上为增函数， 求a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知函数f(x)＝ax(a＞1)，函数g(x)的图象与f(x)的图象关于直线y＝x对称，则函数g(x2)是


    1. A.
      奇函数且在(0，+∞)上是增函数
    2. B.
      偶函数且在(0，+∞)上是减函数
    3. C.
      奇函数且在(-∞，0)上是增函数
    4. D.
      偶函数且在(-∞，0)上是减函数

    查看答案和解析>>

    同步练习册答案