
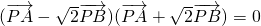 .
.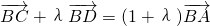 ,求的取值范围.
,求的取值范围.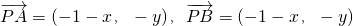
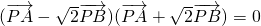 得,
得,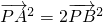 ,即(x+1)2+y2=2x2+2y2,
,即(x+1)2+y2=2x2+2y2, 为半径的圆上,方程为(x-1)2+y2=2.------------------------(4分)
为半径的圆上,方程为(x-1)2+y2=2.------------------------(4分)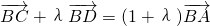 ,
,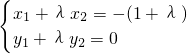 ,∴
,∴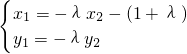 ①,
①,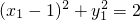 ②,
②,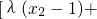 ,
,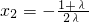 ,
,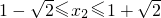 ,∴
,∴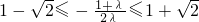 ,
,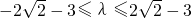 .-----------------------(12分)
.-----------------------(12分)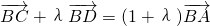 ,确定坐标之间的关系,再结合圆的方程门禁卡求得结论.
,确定坐标之间的关系,再结合圆的方程门禁卡求得结论.

科目:高中数学 来源: 题型:
| PA |
| 2 |
| PB |
| PA |
| 2 |
| PB |
| BC |
| BD |
| BA |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修2) 2009-2010学年 第21期 总177期 人教课标高一版 题型:044
已知平面上两点A(4,1)和B(3,3),在直线l:3x-y-1=0上找一点M,使|MA|+|MB|最小,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com