
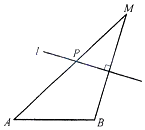
 如图,已知A、B是两个顶点,且$AB=2\sqrt{3}$,动点M到点A的距离是4,线段MB的垂直平分线l交MA于点P.
如图,已知A、B是两个顶点,且$AB=2\sqrt{3}$,动点M到点A的距离是4,线段MB的垂直平分线l交MA于点P.分析 (1)根据题意画出图形,利用垂直平分线转换线段的关系得到PA+PB=4,据椭圆的定义即可得到动点P的轨迹方程.
(2)利用基本不等式,即可得出结论.
解答 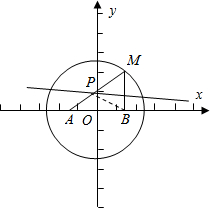 解:(1)以线段AB的中点为坐标原点,直线AB为x轴,线段AB的中点为原点,建立直角坐标系.
解:(1)以线段AB的中点为坐标原点,直线AB为x轴,线段AB的中点为原点,建立直角坐标系.
由线段MB的垂直平分线l交MA于点P知,PB=PM
故PA+PB=PA+PM=AM=4,$AB=2\sqrt{3}$,A($-\sqrt{3}$,0)
,B($\sqrt{3}$,0),即P点的轨迹为以A、B为焦点的椭圆,
中心为(0,0),可得a=2,c=$\sqrt{3}$,则b=1
故P点的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)设l:y=x+m并代入$\frac{{x}^{2}}{4}+{y}^{2}=1$
得5x2+8mx+4m2-4=0,
∵△=(8m)2-4×5×(4m2-4)>0
∴80-16m2>0
即m∈(-$\sqrt{5}$,$\sqrt{5}$),
|PQ|=$\sqrt{1+{1}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}×\sqrt{(-{\frac{8m}{5})}^{2}-4×\frac{4{m}^{2}-4}{5}}$=$\frac{4\sqrt{10-2{m}^{2}}}{5}$
又原点O到直线l的距离为d=$\frac{|m|}{\sqrt{2}}$
∴S△OPQ=$\frac{1}{2}$×$\frac{|m|}{\sqrt{2}}×\frac{4\sqrt{2}\sqrt{5-{m}^{2}}}{5}$=$\frac{2}{5}\sqrt{{m}^{2}(5-{m}^{2})}$≤2×$\frac{2}{5}•\sqrt{(\frac{{m}^{2}+5-{m}^{2}}{2})^{2}}$=2,
当且仅当5-m2=m2即m=±$\frac{\sqrt{10}}{2}$时等号成立,
故△OPQ面积的最大值为:2.
此时直线l的方程:y=x$±\frac{\sqrt{10}}{2}$.
点评 本题考查曲线轨迹方程的求法,直线与圆锥曲线的关系,弦长公式的应用,点到直线的距离,三角形的面积公式与基本不等式的应用,考查计算能力,转化思想的应用,注意轨迹方程中不满足题意的点需要去掉.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 2 | C. | -2 | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| B. | ①分层抽样,②系统抽样,③简单随机抽样 | |
| C. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| D. | ①简单随机抽样,②分层抽样,③系统抽样 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com