
(1)A1C1与BC;(2)A1C1与B1C;(3)A1C1与EF.
思路解析:将异面直线平移成相交直线.
解:(1)∵BC∥B1C1,
∴A1C1与B1C1所成的锐角就是A1C1与BC所成的角.
∵∠A1C1B1=45°,
∴A1C1与BC所成的角是45°.
(2)∵B1C∥A1D,
∴A1C1与A1D所成的锐角就是A1C1与B1C所成的角.
在△A1C1D中,
∵A1C1=A1D=C1D,
∴∠C1A1D=60°,即A1C1与B1C所成的角是60°.
(3)∵EF是△ABD的中位线,
∴EF∥BD.
又BD∥B1D1,
∴B1D1∥EF.
∵A1C1⊥B1D1,
∴A1C1与EF所成的角是90°.
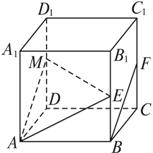
巧妙变式:如下图,在正方体ABCD—A1B1C1D1中,E、F分别是BB1、CC1的中点,求异面直线AE和BF所成角的余弦值.

思路解析:取DD1的中点M,利用余弦定理,通过解△AEM,求得∠EAM的大小,即为两条异面直线所成的角.
方法归纳 构造异面直线所成角的方法常有:
(1)过其中一条直线上的已知点(往往是特殊点),作另一条直线的平行线,使异面直线所成角转化为相交直线所成的角(空间问题转化为平面问题);
(2)当异面直线依附于某几何体,且直接对异面直线平移有困难时,可利用该几何体的特殊点,将两条异面直线分别平移相交于该点;
(3)通过构造辅助平面、辅助几何体来平移直线.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
 如图,已知正方体ABCD-A1B1C1D1中,E、F分别为D1C1、B1C1的中点,AC∩BD=P,A1C1∩EF=Q,若A1C交平面DBFE于R点,试确定R点的位置.
如图,已知正方体ABCD-A1B1C1D1中,E、F分别为D1C1、B1C1的中点,AC∩BD=P,A1C1∩EF=Q,若A1C交平面DBFE于R点,试确定R点的位置.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知正方体ABCD-A1B1C1D1中,E、F分别为D1C1、B1C1的中点,AC∩BD=P,A1C1∩EF=Q,若A1C交平面DBFE于R点,试确定R点的位置.
如图,已知正方体ABCD-A1B1C1D1中,E、F分别为D1C1、B1C1的中点,AC∩BD=P,A1C1∩EF=Q,若A1C交平面DBFE于R点,试确定R点的位置.查看答案和解析>>
科目:高中数学 来源:《第4章 圆与方程》2013年单元测试卷(1)(解析版) 题型:解答题
 如图,已知正方体ABCD-A'B'C'D'的棱长为a,M为BD'的中点,点N在AC'上,且|A'N|=3|NC'|,试求MN的长.
如图,已知正方体ABCD-A'B'C'D'的棱长为a,M为BD'的中点,点N在AC'上,且|A'N|=3|NC'|,试求MN的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com