
【题目】如图所示,在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
(Ⅰ)若BM=2MP,求证:PD∥平面MAC;
(Ⅱ)若平面PAB⊥平面ABCD,平面PAD⊥平面ABCD,求证:PA⊥平面ABCD;
(Ⅲ)在(Ⅱ)的条件下,若二面角B﹣AC﹣M的余弦值为 ![]() ,求
,求 ![]() 的值.
的值.
【答案】证明:(Ⅰ)连结BD交AC于点O,连结OM.
因为 AB∥CD,AB=2CD,所以 ![]() .
.
因为 BM=2MP,所以 ![]() .所以
.所以 ![]() .
.
所以OM∥PD.
因为 OM平面MAC,PD平面MAC,
所以 PD∥平面MAC.
(Ⅱ)因为 平面PAD⊥平面ABCD,AD⊥AB,
平面PAD∩平面ABCD=AD,AB平面ABCD,
所以AB⊥平面PAD.
因为PA平面PAD,所以AB⊥PA.
同理可证:AD⊥PA.
因为 AD平面ABCD,AB平面ABCD,AD∩AB=A,
所以PA⊥平面ABCD.
解:(Ⅲ)分别以边AD,AB,AP所在直线为x,y,z轴,
建立如图所示的空间直角坐标系.
由AB=AD=AP=2CD=2,
得A(0,0,0),B(0,2,0),C(2,1,0),D(2,0,0),P(0,0,2),
则 ![]() ,
, ![]() .
.
由(Ⅱ)得:PA⊥平面ABCD.
所以 平面ABCD的一个法向量为 ![]() .
.
设 ![]() (0≤λ≤1),即
(0≤λ≤1),即 ![]() .所以
.所以 ![]() .
.
设平面AMC的法向量为 ![]() ,
,
则 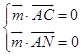 ,即
,即 
令x=λ﹣1,则y=2﹣2λ,z=﹣2λ.所以 ![]() .
.
因为 二面角B﹣AC﹣M的余弦值为 ![]() ,
,
所以 ![]() ,解得
,解得 ![]() .
.
所以 ![]() 的值为
的值为 ![]() .
.

【解析】(Ⅰ)连结BD交AC于点O,连结OM,推导出OM∥PD,由此能证明PD∥平面MAC.(Ⅱ)推导出AB⊥PA,AD⊥PA,由此能证明PA⊥平面ABCD.(Ⅲ)分别以边AD,AB,AP所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出 ![]() 的值.
的值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】△ABC中,角A、B、C所对的边分别为a、b、c,且2acosB=3b﹣2bcosA. 
(1)求 ![]() 的值;
的值;
(2)设AB的中垂线交BC于D,若cos∠ADC= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() . 以坐标原点
. 以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求直线![]() 的参数方程(设参数为
的参数方程(设参数为![]() )和曲线
)和曲线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则b+c的取值范围为( )
,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则b+c的取值范围为( )
A.(﹣∞,3)
B.(0,3]
C.[0,3]
D.(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的短轴长为2,离心率e=
=1(a>b>0)的短轴长为2,离心率e= ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=kx+m与椭圆交于不同的两点A,B,与圆x2+y2= ![]() 相切于点M.
相切于点M.
(i)证明:OA⊥OB(O为坐标原点);
(ii)设λ= ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6 ![]() ,则BC的长为 .
,则BC的长为 . 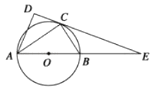
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com