
已知平面内一动点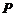 到点
到点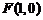 的距离等于它到直线
的距离等于它到直线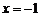 的距离.
的距离.
(Ⅰ)求动点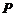 的轨迹
的轨迹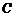 的方程;
的方程;
(Ⅱ)若直线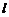 与曲线
与曲线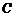 交于
交于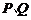 两点,且
两点,且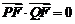 ,又点
,又点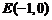 ,求
,求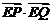 的最小值.
的最小值.
【解】(Ⅰ)依题知动点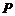 的轨迹是以
的轨迹是以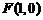 为焦点,以直线
为焦点,以直线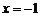 为准线的抛物线,……1分
为准线的抛物线,……1分
所以其标准方程为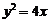 …………………………4分
…………………………4分
(Ⅱ)设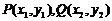 ,则
,则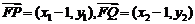
因为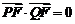 ,所以
,所以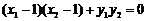
即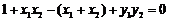 (※)………………………6分
(※)………………………6分
又设直线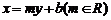 ,代入抛物线
,代入抛物线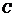 的方程得,
的方程得,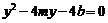
所以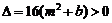 ,且
,且 …………………8分
…………………8分
也所以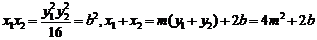 ,
,
所以(※)式可化为,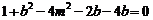 ,
,
即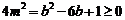 ,得
,得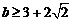 ,或
,或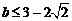 …………………
……10分
…………………
……10分
此时 恒成立.
恒成立.
又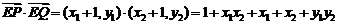 ,且
,且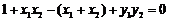 ,
,
所以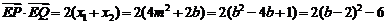
由二次函数单调性可知,当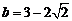 时,
时,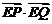 有最小值
有最小值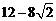 .………
……13分
.………
……13分
〖二法〗设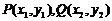 ,则
,则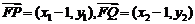
因为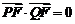 ,所以
,所以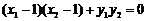
即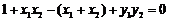 (※)………………………6分
(※)………………………6分
(i)若直线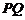 斜率不存在时,则
斜率不存在时,则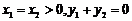 ,
,
代入(※)式得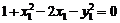 ,又
,又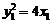 ,
,
所以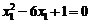 ,即
,即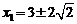 ,
,
所以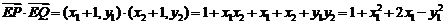
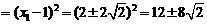 …………………9分
…………………9分
(ii)当直线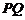 斜率存时,设直线
斜率存时,设直线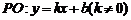 ,
,
代入抛物线方程消去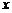 得,
得,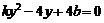
所以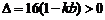 ,且
,且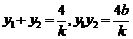 ……………10分
……………10分
所以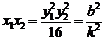 ,
,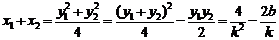
所以(※)式可化为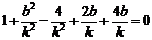
即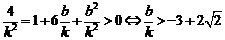 ,或
,或 ……………12分
……………12分
又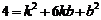 ,知
,知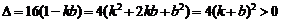 恒成立.(
恒成立.( )
)
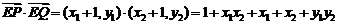 ,且
,且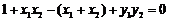 ,
,
所以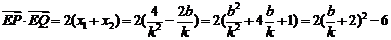
由二次函数单调性可知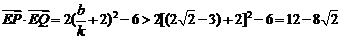
综上(i)(ii)知, 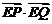 有最小值
有最小值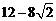 .…………………………13分
.…………………………13分


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源: 题型:
已知平面内一动点![]() 到点F(1,0)的距离与点
到点F(1,0)的距离与点![]() 到
到![]() 轴的距离的等等于1.
轴的距离的等等于1.
(I)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(II)过点![]() 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线![]() ,设
,设![]() 与轨迹
与轨迹![]() 相交于点
相交于点![]() ,
,![]() 与轨迹
与轨迹![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011年湖南省普通高等学校招生统一考试文科数学 题型:解答题
.已知平面内一动点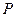 到点F(1,0)的距离与点
到点F(1,0)的距离与点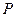 到
到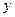 轴的距离的等等于1.
轴的距离的等等于1.
(I)求动点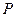 的轨迹
的轨迹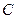 的方程;
的方程;
(II)过点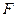 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线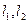 ,设
,设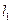 与轨迹
与轨迹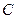 相交于点
相交于点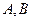 ,
,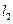 与轨迹
与轨迹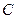 相交于点
相交于点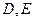 ,求
,求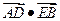 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌10所省高三第二次模拟数学试卷(五)(解析版) 题型:解答题
已知平面内一动点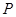 到点
到点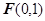 的距离与点
的距离与点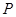 到
到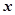 轴的距离的差等于1.(I)求动点
轴的距离的差等于1.(I)求动点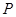 的轨迹
的轨迹 的方程;(II)过点
的方程;(II)过点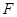 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线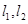 ,设
,设 与轨迹
与轨迹 相交于点
相交于点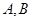 ,
,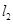 与轨迹
与轨迹 相交于点
相交于点 ,求
,求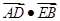 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011年湖南省招生统一考试文科数学 题型:解答题
.已知平面内一动点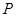 到点F(1,0)的距离与点
到点F(1,0)的距离与点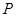 到
到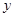 轴的距离的等等于1.
轴的距离的等等于1.
(I)求动点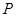 的轨迹
的轨迹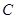 的方程;
的方程;
(II)过点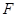 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线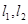 ,设
,设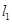 与轨迹
与轨迹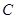 相交于点
相交于点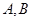 ,
,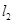 与轨迹
与轨迹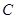 相交于点
相交于点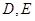 ,求
,求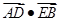 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011年高考试题数学文(湖南卷)解析版 题型:解答题
已知平面内一动点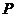 到点F(1,0)的距离与点
到点F(1,0)的距离与点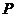 到
到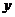 轴的距离的等等于1.
轴的距离的等等于1.
(I)求动点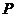 的轨迹
的轨迹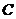 的方程;
的方程;
(II)过点 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线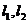 ,设
,设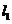 与轨迹
与轨迹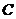 相交于点
相交于点 ,
,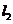 与轨迹
与轨迹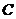 相交于点
相交于点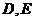 ,求
,求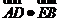 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com