
| 1 |
| 2 |
|
|
|
|
| n(n-1) |
| 2 |
| n2 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
4[1-(-
| ||
1+
|
| 8 |
| 3 |
| 1 |
| 2 |
| n2 |
| 2 |
| 9 |
| 2 |
| 8 |
| 3 |
| 1 |
| 2 |
| n2 |
| 2 |
| 9 |
| 2 |
| 8 |
| 3 |
| 1 |
| 2 |


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
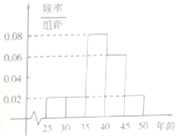 2014年2月7日国务院召开常务会议决定合并新型农村社会养老保险和城镇居民社会养老保险,建立全国统一的城乡居民基本养老保险制度,某街道社区N名居民接受当地电视台就该项制度的采访,他们的年龄在25随至50岁之间.按年龄分5组:[25,30),[30,35),[35,40),[40,45),[45,50],得到的频率分布直方图如图所示,如表是年龄的频数分布表.
2014年2月7日国务院召开常务会议决定合并新型农村社会养老保险和城镇居民社会养老保险,建立全国统一的城乡居民基本养老保险制度,某街道社区N名居民接受当地电视台就该项制度的采访,他们的年龄在25随至50岁之间.按年龄分5组:[25,30),[30,35),[35,40),[40,45),[45,50],得到的频率分布直方图如图所示,如表是年龄的频数分布表.| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 25 | a | b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 数字 | 0 | 1 | 2 | 3 |
| 卡片张数 | 1 | 2 | 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
2
| ||
5+2cos2x-2
|
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| AP |
| BP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3π |
| 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com