
 ="(cosα," sinα), b="(cosβ," sinβ),且
="(cosα," sinα), b="(cosβ," sinβ),且 与b之间满足关系:|k
与b之间满足关系:|k +b|=
+b|=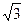 |
| -kb|,其中k>0.
-kb|,其中k>0.  与b的数量积用k表示的解析式f(k);
与b的数量积用k表示的解析式f(k); 能否和b垂直?
能否和b垂直? 能否和b平行?若不能,则说明理由;若能,则求出对应的k值;
能否和b平行?若不能,则说明理由;若能,则求出对应的k值; 与b夹角的最大值。
与b夹角的最大值。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com