
已知向量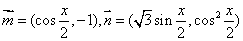 ,设函数
,设函数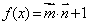
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)在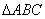 中,角
中,角 、
、 、
、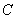 的对边分别为
的对边分别为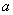 、
、 、
、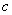 ,且满足
,且满足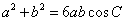 ,
,
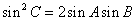 ,求
,求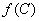 的值.
的值.
科目:高中数学 来源: 题型:
下列有四种说法
①若复数 满足方程
满足方程 ,则
,则 ;②线性回归方程对应的直线
;②线性回归方程对应的直线 一定经过其样本数据点
一定经过其样本数据点 ,
, ,…,
,…, 中的一个点;
中的一个点;
③若 , 则
, 则
 ;
;
④用数学归纳法证明 时,从
时,从 到
到 的证明,左边需增添的一个因式是
的证明,左边需增添的一个因式是 .其中正确的是( ).
.其中正确的是( ).
A.①② B.③ C.③④ D.④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com