练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    对于函数，若为某一三角形的三边长，则称为“可构造三角形函数”．已知函数是“可构造三角形函数”，则实数t的取值范围是（   ）

    A．B．C．D．

    D．

    解析试题分析：由已知得．
    当时，，由，得；当时，显然是“可构造三角形函数”；当时，，则．综上所述：，故选D．
    考点：函数的性质（有界性、最大值和最小值）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    由表格中的数据可以判定方程的一个零点所在的区间是，则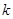的值为（   ）


    		-1
    		0
    		1
    		2
    		3

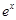    		0．37
    		1
    		2．72
    		7．39
    		20．09

    		1
    		2
    		3
    		4
    		5
    A．-1       B．0         C．1        D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    一次函数的图像过点和，则下列各点在函数的图像上的是(    )

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    定义在R上的函数的图象关于点成中心对称，且对任意的实数x都有f(x)＝－f，f(－1)＝1，f(0)＝－2，则f(1)＋f(2)＋…＋f(2013)＝(　　)

    A．0B．－2
    C．1D．－4

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知函数f(x)是R上的单调增函数且为奇函数,数列{an}是等差数列,a3>0,则f(a1)+f(a3)+f(a5)的值(　　)

    A．恒为正数B．恒为负数
    C．恒为0D．可正可负

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    对实数a和b,定义运算“?”:a?b=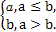设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是(　　)

    A．(-∞,-1)∪(-,0) B．{-1,-}
    C．(-1,-) D．(-∞,-1)∪[-,0)

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图,虚线部分是四个象限的角平分线, 实线部分是函数y=f(x)的部分图象,则f(x)可能是(　　)

    A．x2sinx　　B．xsinx
    C．x2cosx　　D．xcosx

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若偶函数f(x)在(-∞,0)上单调递减,则不等式f(-1)<f(lgx)的解集是(　　)

    A．(0,10) B．(,10)
    C．(,+∞) D．(0,)∪(10,+∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图所示，图(1)反映的是某条公共汽车线路收支差额y与乘客量x之间关系的图像．由于目前该条公交线路亏损，公司有关人员提出两种调整建议，如图(2)(3)所示．
    (注：收支差额＝营业所得的票价收入－付出的成本)

    给出以下说法：
    ①图(2)的建议是：提高成本，并提高票价；
    ②图(2)的建议是：降低成本，并保持票价不变；
    ③图(3)的建议是：提高票价，并保持成本不变；
    ④图(3)的建议是：提高票价，并降低成本．
    其中说法正确的序号是(　　)

    A．①③B．①④C．②③D．②④

    查看答案和解析>>

    同步练习册答案