设曲线C
n:f(x)=x
n+1(n∈N
*)在点
P(-,f(-))处的切线与y轴交于点Q
n(0,y
n).
(Ⅰ)求数列{y
n}的通项公式;
(Ⅱ)设数列{y
n}的前n项和为S
n,猜测S
n的最大值并证明你的结论.
(Ⅰ)∵f′(x)=(n+1)x
n(n∈N
*),(1分)
∴点P处的切线斜率
kn=(n+1)(-)n,(2分)
∴切线方程为:
y-(-)n+1=(n+1)(-)n(x+),(3分)
令x=0得:
yn=(-)n+1+•(-)n,
故数列{y
n}的通项公式为:
yn=•(-)n.(4分)
(Ⅱ)
Sn=•(-)+•(-)2+•(-)3++•(-)n①
两边同乘
-得:
-•Sn=•(-)2+•(-)3+•(-)4++•(-)n+1②
∴得:
•sn=•(-)+•(-)2+•(-)3++•(-)n-•(-)n+1(6分)
∴
3Sn=(-)+(-)2+(-)3++(-)n-n•(-)n+1=
-n•(-)n+1=
--n•(-)n+1∴
Sn=[•(-)n-1](8分)
其中
S1=y1=-,S
2=y
1+y
2=0,
S3=-,
S4=-猜测S
n的最大值为S
2=0.证明如下:(10分)
(i)当n为奇数时,
Sn=-[•()n+1]<0;(11分)
(ii)当n为偶数时,
Sn=•(-1),
设
h(n)=,则
h(n+2)=.
h(n+2)-h(n)=-=-<0,
∴h(n+2)<h(n).(13分)
故
h(n)=的最大值为h(2)=1,即S
n的最大值为S
2=0.(14分)
解法2(Ⅱ)任意k∈N
*,都有y
2k-1<0,y
2k>0;
所以S
n的最大值就是S
2k的最大值.
令
ak=y2k-1+y2k=,显然a
1=0,k>1,a
k<0,
所以S
2k=a
1+a
2++a
k的最大值是S
2=a
1=0.
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
设曲线C
n:f(x)=x
n+1(n∈N
*)在点
P(-,f(-))处的切线与y轴交于点Q
n(0,y
n).
(Ⅰ)求数列{y
n}的通项公式;
(Ⅱ)设数列{y
n}的前n项和为S
n,猜测S
n的最大值并证明你的结论.
查看答案和解析>>
科目:高中数学
来源:2011年广东省东莞高级中学高考数学二模试卷(文科)(解析版)
题型:解答题
设曲线C
n:f(x)=x
n+1(n∈N
*)在点
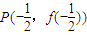
处的切线与y轴交于点Q
n(0,y
n).
(Ⅰ)求数列{y
n}的通项公式;
(Ⅱ)设数列{y
n}的前n项和为S
n,猜测S
n的最大值并证明你的结论.
查看答案和解析>>
科目:高中数学
来源:2011年广东省东莞高级中学高考数学二模试卷(理科)(解析版)
题型:解答题
设曲线C
n:f(x)=x
n+1(n∈N
*)在点
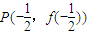
处的切线与y轴交于点Q
n(0,y
n).
(Ⅰ)求数列{y
n}的通项公式;
(Ⅱ)设数列{y
n}的前n项和为S
n,猜测S
n的最大值并证明你的结论.
查看答案和解析>>
科目:高中数学
来源:2010年广东省佛山市高三质量检测数学试卷2(文科)(解析版)
题型:解答题
设曲线C
n:f(x)=x
n+1(n∈N
*)在点
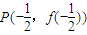
处的切线与y轴交于点Q
n(0,y
n).
(Ⅰ)求数列{y
n}的通项公式;
(Ⅱ)设数列{y
n}的前n项和为S
n,猜测S
n的最大值并证明你的结论.
查看答案和解析>>



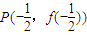 处的切线与y轴交于点Qn(0,yn).
处的切线与y轴交于点Qn(0,yn).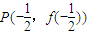 处的切线与y轴交于点Qn(0,yn).
处的切线与y轴交于点Qn(0,yn).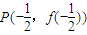 处的切线与y轴交于点Qn(0,yn).
处的切线与y轴交于点Qn(0,yn).