
某校从6名教师中,选派4名同时到3个边远地区支教,每个地区至少选派1名.
(Ⅰ) 共有多少种不同的选派方法?
(Ⅱ) 若6名教师中的甲,乙二位教师不能同时支教,共有多少种不同的选派方法?
(Ⅰ) 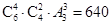 种
(Ⅱ)
种
(Ⅱ) 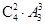 +
+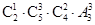 =756种
=756种
【解析】本试题主要是考查了排列组合的运用。
(1)先确定4名人选,然后从中分组分配,利用分步计数乘法原理表示出即可。
(2)分为两种情况,如果甲,乙二位教师都不支教,有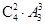 种不同的选派方法
种不同的选派方法
或者甲,乙二位教师恰有一名支教,有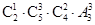 种不同的选派方法,然后借助于分类加法计数原理得到。
种不同的选派方法,然后借助于分类加法计数原理得到。
解:(Ⅰ) 从6名教师中选出4人,有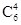 种方法,4名教师选派到3个边远地区支教,每个地区至少选派1名,有
种方法,4名教师选派到3个边远地区支教,每个地区至少选派1名,有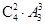 种方法,根据分步计数原理,共有
种方法,根据分步计数原理,共有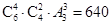 种方法.
种方法.
(Ⅱ) 甲,乙二位教师都不支教,有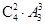 种不同的选派方法
;甲,乙二位教师恰有一名支教,有
种不同的选派方法
;甲,乙二位教师恰有一名支教,有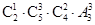 种不同的选派方法. 根据分步计数原理,共有
种不同的选派方法. 根据分步计数原理,共有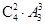 +
+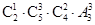 =756种方法
=756种方法


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、150 | B、300 | C、600 | D、900 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com