
若a、b、c>0且a(a+b+c)+bc= ,则2a+b+c的最小值为(
)
,则2a+b+c的最小值为(
)
A. B.
B. C.2
C.2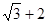 D.2
D.2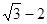
科目:高中数学 来源:2013届内蒙古赤峰市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
若a、b、c是常数,则“a>0且b2-4ac<0”是“对任意x∈R,有ax2+bx+c>0”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013届江西省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
设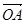 =(1,-2),
=(1,-2),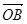 =(a,-1),
=(a,-1),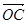 =(-b,0),a>0,b>0,O为坐标原点,若A、B、C三点共线,则
=(-b,0),a>0,b>0,O为坐标原点,若A、B、C三点共线,则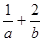 的最小值是( )
的最小值是( )
A.2 B.4 C.6 D.8
查看答案和解析>>
科目:高中数学 来源:新课标高三数学推理与证明专项训练(河北) 题型:选择题
给出下面类比推理命题(其中R为实数集,C为复数集):
①“若a,b∈R,则a-b=0⇒a=b”类比推出“若a,b∈C,则a-b=0⇒a=b”;
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”类比推出“若a,b,c,d∈C,则复数a+bi=c+di⇒a=c,b=d”;
③“若a,b∈R,则a-b>0⇒a>b” 类比推出“若a,b∈C,则a-b>0⇒a>b”;
④“若a,b∈R,则a·b=0⇒a=0或b=0”.类比推出“若a,b∈C,则a·b=0⇒a=0或b=0”.
其中类比结论正确的个数是( )
A.0 B.1
C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com