
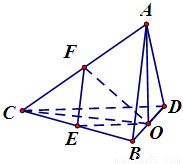
如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=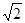 。
。

(1)求证:AO⊥平面BCD;
(2)求E到平面ACD的距离;
(3)求异面直线AB与CD所成角的余弦值。
(1)见解析(2)略(3)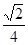
【解析】本题考查点、线、面间的距离的计算,考查空间想象力和等价转化能力,解题时要认真审题,仔细解答,注意化立体几何问题为平面几何问题.
(1)连接OC,由BO=DO,AB=AD,知AO⊥BD,由BO=DO,BC=CD,知CO⊥BD.在△AOC中,由题设知AO=1,CO= 3,AC=2,故AO2+CO2=AC2,由此能够证明AO⊥平面BCD.
(2)利用等体积法得到点到面的距离的求解。
(3)取AC的中点M,连接OM、ME、OE,由E为BC的中点,知ME∥AB,OE∥DC,故直线OE与EM所成的锐角就是异面直线AB与CD所成的角.在△OME中,EM=1能求出异面直线AB与CD所成角大小的余弦.
解:(1)证明:在三角形ABC中,因为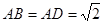 ,O是BD中点,
,O是BD中点,
所以AO⊥BD,且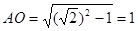 ------------------2分
------------------2分
连结CO,在等边三角形BCD中易得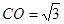 ,
,
所以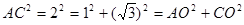
所以AO⊥CO -----------------4分
因为CO∩BD=O,CO、BD 平面BCD
平面BCD
所以AO⊥平面BCD ---------------------6分
(3)分别取BC、AC的中点E、F,连结EF、EG
因为
所以∠FEO或其补角就是异面直线AB、CD所成的角---------8分
连结FO,因为AO⊥平面BCD,所以AO⊥CO,
所以在Rt△ACO中,斜边AC上的中线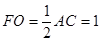 ,
,
又因为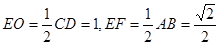 ,
,
所以在△EFO中,
因为 >0,所以异面直线AB、CD所成的角的余弦值是
>0,所以异面直线AB、CD所成的角的余弦值是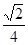 ---------14分
---------14分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
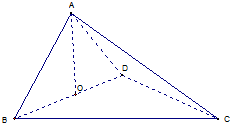 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.查看答案和解析>>
科目:高中数学 来源: 题型:
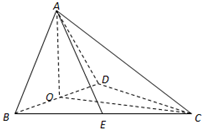 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com