
【题目】(本小题满分12分)
如图,四棱锥![]() 的底面
的底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
,![]() ,
,
![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() .
.
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】.证明:(Ⅰ)∵四边形![]() 是菱形,
是菱形,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() .
.
又![]() , ∴
, ∴![]() .…………………2分
.…………………2分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]()
![]() .又∵
.又∵![]() ,
,
∴![]() 平面
平面![]() ,………………………………………4分
,………………………………………4分
又∵![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() . ………………………………6分
. ………………………………6分
(Ⅱ)解法一:由(1)知![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ………………………6分
………………………6分
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
由(Ⅰ)知![]() ,又
,又![]()
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .…………………………8分
.…………………………8分
∴平面![]() 是平面
是平面![]() 与平面
与平面![]() 的公垂面.
的公垂面.
所以,![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成的锐二面角的平面角.……9分
所成的锐二面角的平面角.……9分
在![]() 中,
中,![]() ,即
,即![]() .……………10分
.……………10分
又![]() ,
,
∴![]() .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .…………12分
.…………12分
理(Ⅱ)解法二:以![]() 为原点,
为原点,![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴的正方向,
轴的正方向,
建立空间直角坐标系![]() ,如图.
,如图.
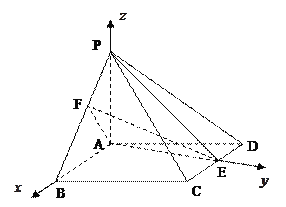
因为![]() ,
,![]() ,∴
,∴![]() 、
、![]() 、
、![]() 、
、![]() 6分
6分
则![]() ,
,![]() ,
,![]() .………7分
.………7分
由(Ⅰ)知![]() 平面
平面![]() ,
,
故平面![]() 的一个法向量为
的一个法向量为![]() .……………………8分
.……………………8分
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则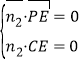 ,即
,即![]() ,令
,令![]() ,
,
则![]() . …………………10分
. …………………10分
∴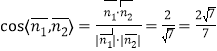 .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .……………12分
.……………12分
【解析】
试题分析:(Ⅰ)∵四边形![]() 是菱形,
是菱形,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() .
.
又![]() , ∴
, ∴![]() .…………………2分
.…………………2分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]()
![]() .又∵
.又∵![]() ,
,
∴![]() 平面
平面![]() ,………………………………………4分
,………………………………………4分
又∵![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() . ………………………………6分
. ………………………………6分
(Ⅱ)解法一:由(1)知![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ………………………7分
………………………7分
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
由(Ⅰ)知![]() ,又
,又![]()
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .…………………………9分
.…………………………9分
∴平面![]() 是平面
是平面![]() 与平面
与平面![]() 的公垂面.
的公垂面.
所以,![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成的锐二面角的平面角.……10分
所成的锐二面角的平面角.……10分
在![]() 中,
中,![]() ,即
,即![]() .……………11分
.……………11分
又![]() ,
,
∴![]() .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .…………14分
.…………14分
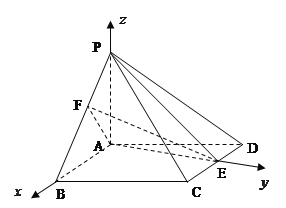
理(Ⅱ)解法二:以![]() 为原点,
为原点,![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,如图所示.因为
,如图所示.因为![]() ,
,![]() ,所以,
,所以,
![]() 、
、![]() 、
、![]() 、
、![]() ,…………7分
,…………7分
则![]() ,
,![]() ,
,![]() .………8分
.………8分
由(Ⅰ)知![]() 平面
平面![]() ,
,
故平面![]() 的一个法向量为
的一个法向量为![]() .……………………9分
.……………………9分
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则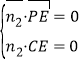 ,即
,即![]() ,令
,令![]() ,
,
则![]() . …………………11分
. …………………11分
∴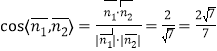 .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .……14分
.……14分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知正四棱柱ABCD﹣A1B1C1D1(底面是正方形,侧棱垂直于底面)的8个顶点都在球O的表面上,AB=1,AA1′=2,则球O的半径R=;若E,F是棱AA1和DD1的中点,则直线EF被球O截得的线段长为 . 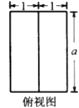
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高考数学试题中共有10道选择题,每道选择题都有4个选项,其中有且仅有一个是正确的.评分标准规定:“每题只选1项,答对得5分,不答或答错得0分.”某考生每道题都给出了一个答案,已确定有6道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
(1)得50分的概率;
(2)得多少分的可能性最大;
(3)所得分数ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:
①集合![]() 与集合
与集合![]() 是相等集合;
是相等集合;
②不存在实数![]() ,使
,使![]() 为奇函数;
为奇函数;
③若![]() ,且f(1)=2,则
,且f(1)=2,则![]() ;
;
④对于函数![]()
![]() 在同一直角坐标系中,若
在同一直角坐标系中,若![]() ,则函数
,则函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
⑤对于函数![]()
![]() 在同一直角坐标系中,函数
在同一直角坐标系中,函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称;其中正确说法是____________.
对称;其中正确说法是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:在△ABC中,若AB<BC,则sinC<sinA;命题q:已知a∈R,则“a>1”是“ ![]() <1”的必要不充分条件.在命题p∧q,p∨q,(¬p)∨q,(¬p)∧q中,真命题个数为( )
<1”的必要不充分条件.在命题p∧q,p∨q,(¬p)∨q,(¬p)∧q中,真命题个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凸四边形PABQ中,其中A,B为定点,AB= ![]() ,P,Q为动点,满足AP=PQ=QB=1.
,P,Q为动点,满足AP=PQ=QB=1.
(1)写出cosA与cosQ的关系式;
(2)设△APB和△PQB的面积分别为S和T,求S2+T2的最大值,以及此时凸四边形PABQ的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com