考点:二面角的平面角及求法,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(Ⅰ)首先根据线面垂直的性质定理,进一步求出线线垂直,AA1⊥平面ABCD,AA1⊥BD,AC⊥BD然后求出BD⊥平面A1ACC1,进一步求出直线 A1B 与平面ACC1A1所成的角为∠BA1O,通过运算求出夹角的大小.
(Ⅱ)利用(Ⅰ)的结论,BD⊥平面A1ACC1,进一步求出:AO⊥BD,A1O⊥BD,二面角 A1-BD-A 的平面角为∠A1OA,然后通过解直角三角形二面角 A1-BD-A 平面角的正切值.
解答:
解:(Ⅰ)连结A
1O
在棱长为a的正方体 ABCD-A
1B
1C
1D
1 中,AC 与BD相交于点O.
∵AA
1⊥平面ABCD,
∴AA
1⊥BD,AC⊥BD
BD⊥平面A
1ACC
1直线 A
1B 与平面ACC
1A
1所成的角为∠BA
1O
在Rt△A
1OB中,
由于正方体的棱长为a
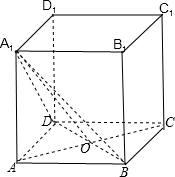
进一步求出:
A1B=a,BO=
asin∠BA
1O=
=
所以:∠BA
1O=30°
则:直线 A
1B 与平面ACC
1A
1所成的角为30°
(Ⅱ)由(Ⅰ)可知:BD⊥平面A
1ACC
1∴AO⊥BD,A
1O⊥BD
二面角 A
1-BD-A 的平面角为∠A
1OA
由题中的条件求出:AO=
a,AA
1=a
tan∠A
1OA=
=
所以二面角 A
1-BD-A 的正切值为
.
点评:本题考查的知识要点:线面垂直的判定定理和性质定理,线面夹角的平面角的求法,二面角的平面角的求法,特殊角的三角函数值,及相关的运算问题.

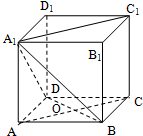 如图,在棱长为a的正方体 ABCD-A1B1C1D1 中,AC 与BD相交于点O.
如图,在棱长为a的正方体 ABCD-A1B1C1D1 中,AC 与BD相交于点O.


 阅读快车系列答案
阅读快车系列答案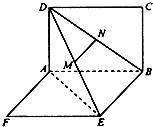 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.线段AB的长为
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.线段AB的长为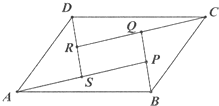 如图,在平行四边形ABCD中,设
如图,在平行四边形ABCD中,设