
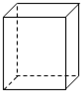
 某公司需制作容积为216ml的长方体形饮料盒,饮料盒底面的长是宽的2倍.当饮料盒底面的宽为多少时,才能使它的用料最省?
某公司需制作容积为216ml的长方体形饮料盒,饮料盒底面的长是宽的2倍.当饮料盒底面的宽为多少时,才能使它的用料最省?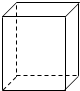 解:设饮料盒底面的宽为x cm,高为h cm,则底面长为2x cm.
解:设饮料盒底面的宽为x cm,高为h cm,则底面长为2x cm.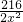 .
.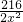 )=4(x2+
)=4(x2+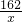 )(x>0),
)(x>0), )=0,得x=
)=0,得x= .
.  时,S′(x)<0,函数S(x) 在(0,
时,S′(x)<0,函数S(x) 在(0, )是减函数;
)是减函数; 时,S′(x)>0,函数S(x) 在(
时,S′(x)>0,函数S(x) 在( ,+∞)是增函数.
,+∞)是增函数. 时,S(x)取得极小值,且是最小值.
时,S(x)取得极小值,且是最小值. cm时,才能使它的用料最省.
cm时,才能使它的用料最省.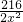 .用料最省,即长方体表面积最小,利用导数即可求得其最小值.
.用料最省,即长方体表面积最小,利用导数即可求得其最小值.

科目:高中数学 来源:2011-2012学年江苏省南京市高二(上)期末数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com