Question

某厂有一批长为18米的条形钢板，可以割成1.8米和1.5米长的零件，它们的加工费分别为1元和0.6元，售价分别为20元和15元，总加工费要求不超过8元，问如何下料能获得最大利润？

Answer 1

答案：
解析：

本小题考查线性规划应用中的最优整点解． 　　解：设割成的1.8米和1.5米长的零件分别为x个、y个，最大利润为z元． 　　则z＝20x＋15y－(x＋)y， 　　即z＝19x＋14.4y(x、y∈N)． 　　且由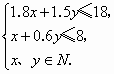： 　　作出不等式组表示的平面区域，如图． 　　由 　　解得M(，)，而，N． 　　∵x、y为自然数，在可行域内找出与点M最近的点为(3，8)． 　　此时z＝19×3＋14.4×8＝172.2(元) 　　又过可行域的另一顶点(0，12)处，z＝19×0＋14.4×12＝172.8(元) 　　过可行域中顶点(8，0)时，z＝19×8＋14.4×0＝152(元)． 　　∴当x＝0，y＝12时，z＝172.8元为最大值． 　　答：只要截1.5米长的零件12个，就能获得最大利润．