解:(Ⅰ)f(x)当x∈(-∞,1]时有意义的条件是1+2
x+…+(n-1)
x+n
xa>0,x∈(-∞,1],n≥2,
即
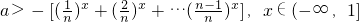
,
∵
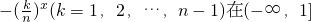
上都是增函数,
∴
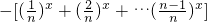
在(-∞,1]上也是增函数,
从而它在x=1时取得最大值
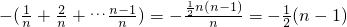
.
所以
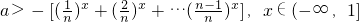
,
∵
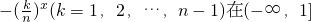
等价于
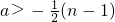
,
故a的取值范围是{a|a>-
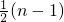
}.
(Ⅱ)证明:只需证明n≥2时,[1+2
x+…+(n-1)
x+n
xa]
2
<n[1+2
2x+…+(n-1)
2x+n
2xa],a∈(0,1],x≠0.
∵(a
1+a
2+…+a
n2)
2=(a
12+a
22+…a
n2)+2(a
1a
2+a
2a
3+…+a
n-1a
n)
≤(a
12+a
22+…a
n2)+[(a
12+a
22)+…+(a
12+a
n2)]+[(a
22+a
32)
+…+(a
22+a
n2)]+…+[(a
n-22+a
n-12)+(a
n-22+a
n2)]+(a
n-12+a
n2)
=n(a
12+a
22+…+a
n2).
于是(a
1+a
2+…+a
n)
2≤n(a
12+a
22+…+a
n2)当a
1=a
2=…=a
n时成立.
利用上面结果知,当a=1,x≠0时,因1≠2
x,
所以有[1+2
x+…+(n-1)
x+n
xa]
2<n[1+2
2x+…+(n-1)
2x+n
2xa],a∈(0,1],
当0<a<1,x≠0时,因a
2<a,
所以有[1+2
x+…+(n-1)
x+n
xa]
2<n[1+2
2x+…+(n-1)
2x+n
2xa],
即有2f(x)<f(2x)a∈(0,1],x≠0.
分析:(Ⅰ)、f(x)当x∈(-∞,1]时有意义的条件是1+2
x+…+(n-1)
x+n
xa>0,x∈(-∞,1],n≥2,即
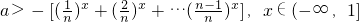
,然后由函数的单调性求实数a的取值范围.
(Ⅱ)、欲证如果a∈(0,1],证明2f(x)<f(2x)当x≠0时成立,只需证明n≥2时,[1+2
x+…+(n-1)
x+n
xa]
2<n[1+2
2x+…+(n-1)
2x+n
2xa],a∈(0,1],x≠0即可得证.
点评:本题是比较难的对数函数的综合题,在解题过程中要注意等价转化思想的灵活运用,并且细心运算,避免不必要的错误.

 ,其中a是实数,n是任意自然数且n≥2.
,其中a是实数,n是任意自然数且n≥2.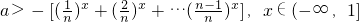 ,
,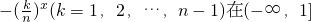 上都是增函数,
上都是增函数,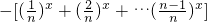 在(-∞,1]上也是增函数,
在(-∞,1]上也是增函数,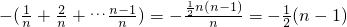 .
.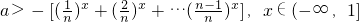 ,
,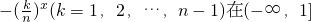 等价于
等价于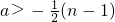 ,
,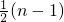 }.
}.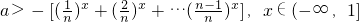 ,然后由函数的单调性求实数a的取值范围.
,然后由函数的单调性求实数a的取值范围.

 ,其中a为常数,若当x∈(-∞,1]时,f(x)有意义,求实数a的取值范围.
,其中a为常数,若当x∈(-∞,1]时,f(x)有意义,求实数a的取值范围. ,其中a是实数,n是任意自然数且n≥2.
,其中a是实数,n是任意自然数且n≥2.