
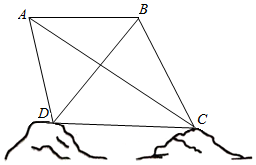
 Ϊ���ƺ���òͼ��������������C��D֮��ľ��룬����̽������ˮƽ������A��B������в�����A��B��C��D��ͬһ��Ǧ��ƽ���ڣ�����̽���Dz�á�BAC=30�㣬��DAC=45�㣬��ABD=45�㣬��DBC=75�㣬A��B����ľ���Ϊ$\sqrt{3}$�����C��D֮��ľ���Ϊ��������
Ϊ���ƺ���òͼ��������������C��D֮��ľ��룬����̽������ˮƽ������A��B������в�����A��B��C��D��ͬһ��Ǧ��ƽ���ڣ�����̽���Dz�á�BAC=30�㣬��DAC=45�㣬��ABD=45�㣬��DBC=75�㣬A��B����ľ���Ϊ$\sqrt{3}$�����C��D֮��ľ���Ϊ��������| A�� | $\sqrt{5}$���� | B�� | 2���� | C�� | $\frac{\sqrt{6}+\sqrt{2}}{2}$���� | D�� | $\sqrt{2}$+1 |
���� �����ADB���ڡ�ABD�У������Ҷ�������BD�����жϡ�ABCΪ���������Σ�����BC����BCD�У������Ҷ�������CD��
��� �⣺��ADB=180��-30��-45��-45��=60�㣬
�ڡ�ABD�У������Ҷ�������BD=$\frac{\sqrt{3}sin75��}{sin60��}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$��
��ABC�У���ACB=180��-30��-45��-75��=30�㣬
��BC=BA=$\sqrt{3}$��
��BCD�У������Ҷ�������CD2=BC2+BD2-2BC•BDcos��DBC
=3+��$\frac{\sqrt{6}+\sqrt{2}}{2}$��2-2��$\sqrt{3}��$$\frac{\sqrt{6}+\sqrt{2}}{2}$��$\frac{\sqrt{6}-\sqrt{2}}{4}$=5��
��CD=$\sqrt{5}$��
��ѡ��A��
���� ���⿼�����Ҷ��������Ҷ�������Ӧ�ã�����ѧ����������Ķ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -7 | B�� | -6 | C�� | -2 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$ | B�� | $\frac{1}{2}$ | C�� | -2 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��-2�� x��1 } | B�� | {x|-2��x��1 } | C�� | {x|x��-1 ��x��2 } | D�� | {x|-1��x��2 } |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com