练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    .已知正四面体的高为H，它的内切球半径为R，则R︰H＝________.

    1:4
    略
    解：设正四面体的内切圆园心为O,连接O到正四面体的各个顶点，把正四面体分割成四个小的四面体
    则内切圆到各个面的距离就是内切圆的半径R，正四面体的体积可以表示为：
    S正四面体=4*（1/3*S底面积*R）
    又有S正四面体=1/3*S底面积*H
    所以：4*（1/3*S底面积*R=1/3*S底面积*H
    得：R︰H＝1:4
    故答案为1:4
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知等边三角形ABC的高为h，它的内切圆半径为r，则r：h=1：3，由此类比得：已知正四面体的高为H，它的内切球半径为R，则R：H=
    1：4
    1：4
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南省南阳市高三上学期期终质量评估文科数学 题型：填空题

    ．已知正四面体的高为H，它的内切球半径为R，则R︰H＝______________．

     

    查看答案和解析>>

    科目：高中数学 来源：2012届河南省南阳市高二下学期期末考试文科数学 题型：填空题

    已知等边三角形ABC的高为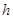，它的内切圆半径为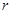，则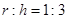，由此类比得：已知正四面体的高为H，它的内切球半径为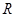，则      ．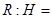

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知等边三角形ABC的高为h，它的内切圆半径为r，则r：h=1：3，由此类比得：已知正四面体的高为H，它的内切球半径为R，则R：H=______．

    查看答案和解析>>

    同步练习册答案