在120°的二面角P-a-Q的两个面P和Q内,分别有点A和点B 已知点A和点B到棱a的距离分别为2和4,且线段AB=10,
(1)求直线AB和棱a所成的角;
(2)求直线AB和平面Q所成的角.
解:(1)在平面P内作直线AD⊥a于点D,在平面Q内,作直线BE⊥a于点E,
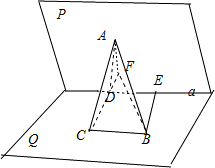
从点D作a的垂线与从点B作a的平行线相交于点C.
∴∠ABC等于AB和a所成的角,
∠ADC为两面角P-a-Q的平面角,
∴∠ADC=120°,
又AD=2,BCDE为矩形,∴CD=BE=4.
连接AC,由余弦定理得AC
2=AD
2+CD
2-2AD•CDcos∠ADC=2
2+4
2-2×2×4×cos120°=28.
∴
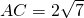
.
又∵AD⊥a,CD⊥a,∴a⊥平面ACD,
∵BC∥a,∴BC⊥平面ACD,
∴BC⊥AC.
在直角△ABC中,
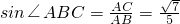
,
∴

.
(2)在△ACD所在的平面内,作AF⊥CD交CD的延长线于点F.
∵平面ACD⊥平面Q,∴AF⊥平面Q.
在△ADF中,∠ADF=60°,AD=2,∴AF=
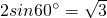
.
连接BF,于是∠ABF是AB和平面Q所成的角,
在△ABF为直角三角形,
∴
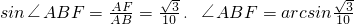
.
分析:(1)如图所示,在平面P内作直线AD⊥a于点D,在平面Q内,作直线BE⊥a于点E,过点D作DC⊥a,与从点B作CB∥a相交于点C.∠ABC等于AB和a所成的角,∠ADC为两面角P-a-Q的平面角,
利用余弦定理即可得到AC,由a⊥平面ACD,BC∥a即可得到BC⊥平面ACD,在直角△ABC中求出sin∠ABC即可;
(2)在△ACD所在的平面内,作AF⊥CD交CD的延长线于点F,利用面面垂直的性质即可证明AF⊥平面Q,从而得到∠ABF是直线AB和平面Q所成的角.
点评:熟练掌握线面与面面垂直的判定和性质定理、线面角、异面直线所成的角、余弦定理及常作的辅助线是解题的关键.


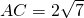 .
.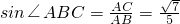 ,
, .
.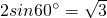 .
.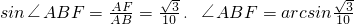 .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案