
| 品种 | 电能(千度) | 煤(吨) | 工人人数(人) | 产值(万元) |
| 甲 | 2 | 3 | 5 | 7 |
| 乙 | 8 | 5 | 2 | 10 |
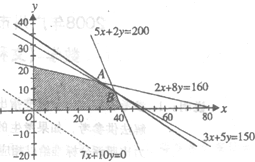 解:设甲、乙两种产品每天分别生产x吨和y吨,
解:设甲、乙两种产品每天分别生产x吨和y吨,
|
|
|
|
|
| 200 |
| 7 |
| 90 |
| 7 |
| 700 |
| 19 |
| 150 |
| 19 |
| 7 |
| 10 |
| 700 |
| 19 |
| 150 |
| 19 |
|
| 6400 |
| 19 |
| 700 |
| 19 |
| 150 |
| 19 |
| 6400 |
| 19 |


科目:高中数学 来源: 题型:
 (2008•广州二模)如图所示,F为双曲线C:
(2008•广州二模)如图所示,F为双曲线C:| x2 |
| 9 |
| y2 |
| 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•广州二模)某校为了了解学生的体育锻炼情况,随机调查了70名学生,得到他们在某一天各自的体育锻炼时间的数据,结果用如图3所示的条形图表示.根据条形图可得这70名学生这一天平均每人的体育锻炼时间为
(2008•广州二模)某校为了了解学生的体育锻炼情况,随机调查了70名学生,得到他们在某一天各自的体育锻炼时间的数据,结果用如图3所示的条形图表示.根据条形图可得这70名学生这一天平均每人的体育锻炼时间为查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com