
分析 (1)由已知条件推导出F1(-1,0),a2+b2=7(a-1)2,b2=a2-1,由此能求出椭圆C1的方程.
(2)设Q,R,P,S各点坐标依次为(x1,y1),(x2,y2),(x3,y3),(x4,y4),将y=kx+b代入椭圆C方程,得:(3+4k2)x2+8kbx+4b2-12=0,将y=kx+b代入椭圆C2方程,得:(3+4k2)x2+8kbx+4b2-36=0,由x1+x2=x3+x4,可得线段PS、QR中点相同,所以|PQ|=|RS|,由$\overrightarrow{PS}+\overrightarrow{RS}=2\overrightarrow{QS}$⇒$\overrightarrow{PQ}=\overrightarrow{QR}$,所以|PS|=3|RQ|,可得:|x3-x4|=3|x1-x2|,由此利用根的判别式、韦达定理、弦长公式结合已知条件能求出k,b.
解答 解:(1)设椭圆C1方程为:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),
∴直线AB方程为:$\frac{x}{-a}+\frac{y}{b}=1$…(1分)
∴F1(-1,0)到直线AB距离为$d=\frac{|b-ab|}{{\sqrt{{a^2}+{b^2}}}}=\frac{{\sqrt{7}}}{7}b$⇒a2+b2=7(a-1)2…(2分)
又b2=a2-1,解得:a=2,$b=\sqrt{3}$…(4分)
故椭圆C方程为:$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(5分)
(2)椭圆C2的方程为:$\frac{x^2}{12}+\frac{y^2}{9}=1$…(6分)
设Q、R、P、S各点坐标依次为(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)
将y=kx+b代入椭圆C方程,得:(3+4k2)x2+8kbx+4b2-12=0
∴${△_1}={(8kb)^2}-4(3+4{k^2})(4{b^2}-12)=48(4{k^2}+3-{b^2})>0$(*)…(7分)
此时:${x_1}+{x_2}=-\frac{8kb}{{3+4{k^2}}}$,${x_1}{x_2}=\frac{{4{b^2}-12}}{{3+4{k^2}}}$$⇒|{x_1}-{x_2}|=\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=\frac{{4\sqrt{3(4{k^2}+3-{b^2})}}}{{3+4{k^2}}}$…(8分)
将y=kx+b代入椭圆C2方程,得:(3+4k2)x2+8kbx+4b2-36=0
∴${x_3}+{x_4}=-\frac{8kb}{{3+4{k^2}}}$,${x_3}{x_4}=\frac{{4{b^2}-36}}{{3+4{k^2}}}$$⇒|{x_3}-{x_4}|=\frac{{4\sqrt{3(12{k^2}+9-{b^2})}}}{{3+4{k^2}}}$…(9分)
∴x1+x2=x3+x4,可得线段PS、QR中点相同,所以|PQ|=|RS|…(10分)
由$\overrightarrow{PS}+\overrightarrow{RS}=2\overrightarrow{QS}$⇒$\overrightarrow{PQ}=\overrightarrow{QR}$,所以|PS|=3|RQ|,可得:|x3-x4|=3|x1-x2|
∴$\frac{4\sqrt{3(12{k}^{2}+9-{b}^{2})}}{3+4{k}^{2}}=3×\frac{4\sqrt{3(4{k}^{2}+3-{b}^{2})}}{3+4{k}^{2}}$⇒12k2+9=4b2(满足(*)式).…(11分)
又∵k2+b2=$\frac{9}{4}$,联立上式得:k=0,b=±$\frac{3}{2}$
故直线PS的方程为$y=±\frac{3}{2}$…(12分)
点评 本题考查了椭圆与直线的位置关系,关键是结合图形把已知转化为可用韦达定理、弦长公式,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 某高校青年志愿者协会,组织大一学生开展一次爱心包裹劝募活动,将派出的志愿者,分成甲、乙两个小组,分别在两个不同的场地进行劝募,每个小组各6人,爱心人士每捐购一个爱心包裹,志愿者就将送出一个钥匙扣作为纪念,茎叶图记录了这两个小组成员某天劝募包裹时送出钥匙扣的个数,且图中乙组的一个数据模糊不清,用x表示,已知甲组送出钥匙扣的平均数比乙组的平均数少一个.
某高校青年志愿者协会,组织大一学生开展一次爱心包裹劝募活动,将派出的志愿者,分成甲、乙两个小组,分别在两个不同的场地进行劝募,每个小组各6人,爱心人士每捐购一个爱心包裹,志愿者就将送出一个钥匙扣作为纪念,茎叶图记录了这两个小组成员某天劝募包裹时送出钥匙扣的个数,且图中乙组的一个数据模糊不清,用x表示,已知甲组送出钥匙扣的平均数比乙组的平均数少一个.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
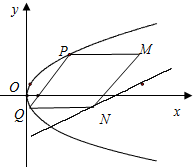 抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然.如图所示,今有抛物线y2=2px(p>0),一光源在点M($\frac{41}{4}$,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线l:2x-4y-17=0上的点N,再反射后又射回点M,设P,Q两点的坐标分别是(x1,y1),(x2,y2),
抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然.如图所示,今有抛物线y2=2px(p>0),一光源在点M($\frac{41}{4}$,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线l:2x-4y-17=0上的点N,再反射后又射回点M,设P,Q两点的坐标分别是(x1,y1),(x2,y2),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠ABC=120°,PD⊥AB,平面PAB⊥平面ABCD,点E,F为棱PB,PC中点,二面角F-AD-C的平面角的余弦值为$\frac{3\sqrt{13}}{13}$.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠ABC=120°,PD⊥AB,平面PAB⊥平面ABCD,点E,F为棱PB,PC中点,二面角F-AD-C的平面角的余弦值为$\frac{3\sqrt{13}}{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 2 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com