
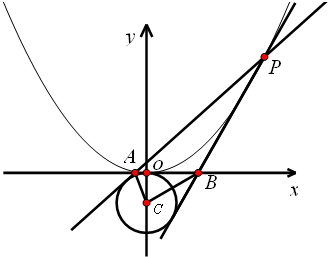
如图,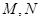 是抛物线
是抛物线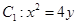 上的两动点(
上的两动点(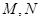 异于原点
异于原点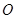 ),且
),且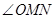 的角平分线垂直于
的角平分线垂直于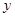 轴,直线
轴,直线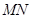 与
与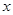 轴,
轴,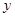 轴分别相交于
轴分别相交于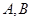 .
.
(1) 求实数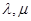 的值,使得
的值,使得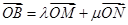 ;
;
(2)若中心在原点,焦点在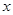 轴上的椭圆
轴上的椭圆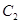 经过
经过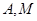 . 求椭圆
. 求椭圆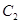 焦距的最大值及此时
焦距的最大值及此时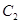 的方程.
的方程.
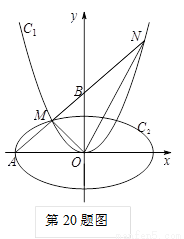
(1)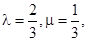 ;(2)
;(2)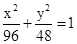 .
.
【解析】本题主要考查直线的斜率、抛物线的切线、两直线平行的位置关系,椭圆的基本性质,考查学生运算能力、推理论证以及分析问题、解决问题的能力,考查数形结合思想、
化归与转化思想.
解: (1) 设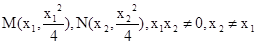
由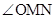 的角平分线垂直于Y轴知,直线OM与直线MN的倾斜角互补,从而斜率之和等于0,即
的角平分线垂直于Y轴知,直线OM与直线MN的倾斜角互补,从而斜率之和等于0,即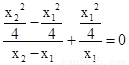 化简得
化简得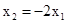 . 3分
. 3分
由点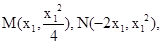 知直线MN的方程为
知直线MN的方程为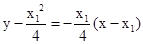 .
.
分别在其中令Y=0及X=0得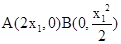 . 5分
. 5分
将B,M,N的坐标代入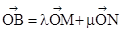 中得
中得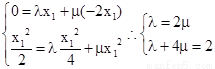 , 7分
, 7分
所以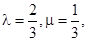 8分
8分
(2) 设椭圆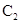 的方程为
的方程为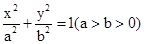 ,
,
将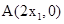 ,
,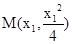 代入,得
代入,得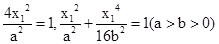 , 9分
, 9分
解得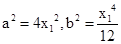 , 由
, 由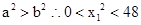 . 10分
. 10分
椭圆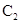 的焦距
的焦距
 12分
12分
当且仅当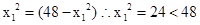 时,上式取等号, 故
时,上式取等号, 故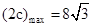 , 13分
, 13分
此时椭圆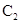 的方程为
的方程为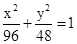 14分
14分


科目:高中数学 来源: 题型:
 已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为2
已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为23
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
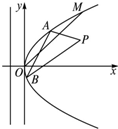 如图,在直角坐标系xOy中,点P(1,
如图,在直角坐标系xOy中,点P(1,| 1 |
| 2 |
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
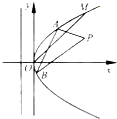 (2012•浙江)如图,在直角坐标系xOy中,点P(1,
(2012•浙江)如图,在直角坐标系xOy中,点P(1,| 1 |
| 2 |
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线![]() (
(![]() ).抛物线上的点
).抛物线上的点![]() 到焦点的距离为2
到焦点的距离为2
(1)求抛物线的方程和![]() 的值;
的值;
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com