
分析 设出以M为中点的弦的两个端点的坐标,代入椭圆的方程相减,把中点公式代入,可得弦的斜率与a,b的关系式.从而求得椭圆的离心率.
解答 解:显然M(-2,1)在椭圆内,设直线与椭圆的交点A(x1,y1),B(x2,y2),
则$\frac{{{x}_{1}}^{2}}{{a}^{2}}+\frac{{{y}_{1}}^{2}}{{b}^{2}}=1$,$\frac{{{x}_{2}}^{2}}{{a}^{2}}+\frac{{{y}_{2}}^{2}}{{b}^{2}}=1$,相减得:$\frac{({x}_{2}-{x}_{1})({x}_{2}+{x}_{1})}{{a}^{2}}$+$\frac{({y}_{2}+{y}_{1})({y}_{2}-{y}_{1})}{{b}^{2}}$=0,
整理得:k=-$\frac{{b}^{2}({x}_{2}+{x}_{1})}{{a}^{2}({y}_{2}+{y}_{1})}$=1,
又弦的中点坐标是(-2,1),
∴$\left\{\begin{array}{l}{x}_{2}+{x}_{1}=-4\\{y}_{2}{+y}_{1}=2\end{array}\right.$,
∴$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,
则椭圆的离心率是e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{2}}{2}$.
椭圆的离心率:$\frac{\sqrt{2}}{2}$.
点评 本题考查椭圆的标准方程和简单性质,中点公式及斜率公式的应用,以及直线方程,属于基础题.本题解题中直接利用点差法巧妙用上了中点坐标公式与弦的斜率,方法极为巧妙,此方法即为通常所说的点差法,研究弦中点问题时经常采用此方法.


科目:高中数学 来源: 题型:选择题
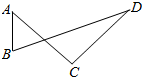
| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{BC}$+$\overrightarrow{DA}$ | B. | $\overrightarrow{AC}$+$\overrightarrow{BD}$=$\overrightarrow{BC}$+$\overrightarrow{AD}$ | C. | $\overrightarrow{AC}$+$\overrightarrow{DB}$=$\overrightarrow{DC}$+$\overrightarrow{BA}$ | D. | $\overrightarrow{AB}$+$\overrightarrow{DA}$=$\overrightarrow{AC}$+$\overrightarrow{DB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,OA是南北方向的一条公路,OB是北偏东45°方向的一条公路,某风景区的一段边界为曲线C.为方便游客光,拟过曲线C上的某点分别修建与公路OA,OB垂直的两条道路PM,PN,且PM,PN的造价分别为5万元/百米,40万元/百米,建立如图所示的直角坐标系xoy,则曲线符合函数y=x+$\frac{{4\sqrt{2}}}{x^2}$(1≤x≤9)模型,设PM=x,修建两条道路PM,PN的总造价为f(x)万元,题中所涉及的长度单位均为百米.
如图,OA是南北方向的一条公路,OB是北偏东45°方向的一条公路,某风景区的一段边界为曲线C.为方便游客光,拟过曲线C上的某点分别修建与公路OA,OB垂直的两条道路PM,PN,且PM,PN的造价分别为5万元/百米,40万元/百米,建立如图所示的直角坐标系xoy,则曲线符合函数y=x+$\frac{{4\sqrt{2}}}{x^2}$(1≤x≤9)模型,设PM=x,修建两条道路PM,PN的总造价为f(x)万元,题中所涉及的长度单位均为百米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2≤0 | B. | ?x0∈R,x${\;}_{0}^{2}$>0 | C. | ?x0∈R,x${\;}_{0}^{2}$<0 | D. | ?x0∈R,x${\;}_{0}^{2}$≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22 | B. | 24 | C. | 26 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 酒驾人数x | 80 | 147 | 121 | 100 | 96 | 103 | 87 |
| 交通事故y | 19 | 31 | 30 | 23 | 25 | 24 | 20 |
| A. | 正相关 | B. | 负相关 | C. | 不相关 | D. | 函数关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com