已知A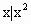＝{-x-2＞0.x∈Z}.B＝{+.且A∩B＝{-2}.求实数k的取值范围．题目和参考答案——青夏教育精英家教网—

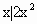已知A＝{－x－2＞0，x∈Z}，B＝{＋(5＋2k)x＋5k＜0，x∈Z)，且A∩B＝{－2}，求实数k的取值范围．

答案：
解析：

解 ∵－x－2＞0的解为x＞2或x＜－1；又由＋(5＋2k)x＋5k＜0，得(x＋k)(2x＋5)＜0．依题意，－k＞－2，即k＜2，∴B＝{x|－＜x＜－k，x∈Z}．由于当x∈Z时，在(，－1)上，A∩B＝{－2}；在[－1，3]上，A∩B＝，∴－2＜－k≤3，即－3≤k＜2．

练习册系列答案

小学教材完全解读系列答案

相关习题

科目：高中数学 来源：浙江省金华一中2011－2012学年高一上学期期中考试数学试题(人教版) 题型：022

给定集合A、B，定义：A*B＝{x|x∈A或x∈B，但xA∩B}，又已知A＝{0，1，2}，B＝{1，2，3}，用列举法写出A*B＝________

科目：高中数学 来源：学习周报　数学　人教课标高二版(A必修5)　2009－2010学年　第12期　总第168期人教课标版(A必修5) 题型：044

已知a＝(1，x)，b＝(x²＋x，－x)，m为实数，求使m(a·b)²－(m＋1)a·b＋1＜0成立的x的取值范围．

科目：高中数学 来源：教材完全解读　高中数学　必修5(人教B版课标版) 人教B版课标版 题型：044

已知a＝(1，x)，b＝(x²＋x，－x)m为常数，且m≤－2，求使a·b＋2＞m成立的x的范围．

科目：高中数学 来源：随堂练1＋2　讲·练·测　高中数学·必修1（苏教版）苏教版 题型：022

已知A＝{－1，－2，a}，B＝{3，4，5}，若f：x→1－2x是从A到B的映射，则a＝________．

科目：高中数学 来源： 题型：

已知a＝(1，x)，b＝(x²＋x，－x)，m为实数，求使m(a·b)²－(m＋1)a·b＋1＜0成立的x的范围.

同步练习册答案