练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     函数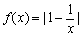（x > 0）

    求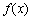的单调减区间并证明；

    是否存在正实数m，n（m < n），使函数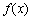的定义域为［m，n］时值域为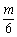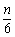［，］？若存在，求m，n的值；若不存在，请说明理由．

     

     

     

     

     

     

     

     

     

     

     

    【答案】

     解：(1) 的单调减区间为 2分

    任取且   3分

    则   4分

         6分

    ∴

    ∴ 在上为减函数 7分

            (2) ①若，则

    ∴

    两式相减，得不可能成立 9分

    ②若，，则的最小值为0，不合题意   10分

    ③若，则

    ∴

    ∴  ∴ m，n为的不等实根

    ∴ ，

    综上，存在，符合题意 12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本题满分12分）已知函数（x>0）．（1）若b≥，求证≥（e是自然对数的底数）；（2）设F(x)=+（x≥1，a∈R），试问函数F(x)是否存在最小值？若存在，求出最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年人教版高考数学文科二轮专题复习提分训练7练习卷（解析版） 题型：填空题

    已知f(x)是定义在R上的奇函数.当x>0时,f(x)=x2-4x,则不等式f(x)>x的解集用区间表示为　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2013年全国普通高等学校招生统一考试理科数学（全国大纲卷解析版） 题型：选择题

    函数（x>0）的反函数=（  ）

    A．    B．     C．     D．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年吉林省高三上学期期末质量检测数学 题型：解答题

    （本题满分14分）

    （理）已知数列{an}的前n项和，且=1，

    .（I）求数列{an}的通项公式；

    （II）已知定理：“若函数f(x)在区间D上是凹函数，x>y(x,y∈D)，且f’(x)存在，则有

    < f’(x)”．若且函数y=xn+1在(0,+∞)上是凹函数，试判断bn与bn+1的大小；

    （III）求证：≤bn<2.

     

    查看答案和解析>>

    科目：高中数学 来源：2010年新课标版高一数学必修一第二章单元测试 题型：选择题

    函数当x>2 时恒有>1，则a的取值范围是                       （    ）

    A．                     B．0

    C．                            D．

     

    查看答案和解析>>

    同步练习册答案