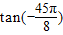【答案】
分析:先利用诱导公式把各个式子中角用锐角来表示,再根据正弦函数、余弦函数、正切函数在(0,
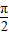
)上的单调性,从而得出结论.
解答:解:由于sin
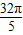
=sin
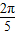
,sin
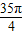
=sin
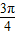
=sin
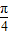
,而且函数y=sinx在(0,
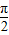
)上是增函数,故sin
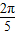
>sin
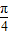
,
∴
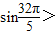
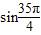
,故A不正确.
由于cos(-1317°)=cos(-4×360°+123°)=cos123°=-cos57°,cos(-112°)=cos112°=-cos68°,而函数y=cosx在(0,
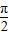
)上是减函数,
故cos68°<cos57°,即-cos68°>-cos57°,∴cos(-1317°)<cos(-112°),故B不正确.
由于

=tan(-2π-
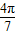
)=-tan
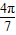
,tan(-
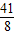
)=tan(-5π-
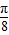
)=-tan
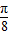
,而函数y=tanx在(0,
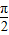
)上是增函数,
故有tan

>tan
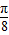
,∴-tan
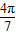
<-tan
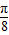
,即
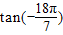
>
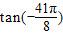
,故C正确.
由于
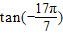
=tan(-2π-
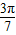
)=-tan
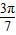
,
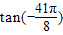
=tan(-5π-
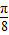
)=-tan
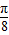
,而函数y=tanx在(0,
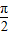
)上是增函数,
故有tan
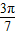
>tan
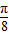
,∴-tan
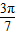
<-tan
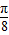
,即
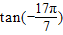
<
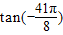
,故D不正确.
故选C.
点评:本题主要考查正弦函数、余弦函数、正切函数在(0,π)上的单调性,诱导公式的应用,属于中档题.

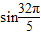 <
<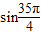
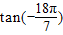 >
>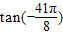
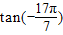 >
>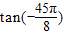
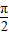 )上的单调性,从而得出结论.
)上的单调性,从而得出结论.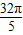 =sin
=sin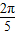 ,sin
,sin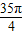 =sin
=sin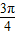 =sin
=sin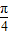 ,而且函数y=sinx在(0,
,而且函数y=sinx在(0,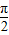 )上是增函数,故sin
)上是增函数,故sin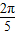 >sin
>sin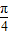 ,
,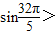
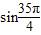 ,故A不正确.
,故A不正确.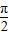 )上是减函数,
)上是减函数, =tan(-2π-
=tan(-2π-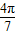 )=-tan
)=-tan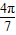 ,tan(-
,tan(-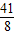 )=tan(-5π-
)=tan(-5π-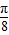 )=-tan
)=-tan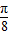 ,而函数y=tanx在(0,
,而函数y=tanx在(0,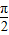 )上是增函数,
)上是增函数, >tan
>tan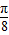 ,∴-tan
,∴-tan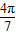 <-tan
<-tan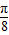 ,即
,即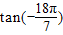 >
>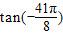 ,故C正确.
,故C正确.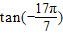 =tan(-2π-
=tan(-2π-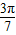 )=-tan
)=-tan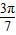 ,
,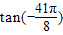 =tan(-5π-
=tan(-5π-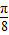 )=-tan
)=-tan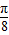 ,而函数y=tanx在(0,
,而函数y=tanx在(0,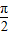 )上是增函数,
)上是增函数,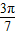 >tan
>tan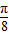 ,∴-tan
,∴-tan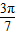 <-tan
<-tan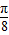 ,即
,即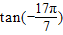 <
<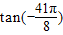 ,故D不正确.
,故D不正确.

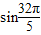 <
<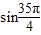
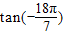 >
>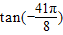
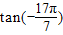 >
>