
分析 由题意设P(x,y),则$\sqrt{(x+c)^{2}+{y}^{2}}•\sqrt{(x-c)^{2}+{y}^{2}}$=a2,即[(x+c)2+y2]•[(x-c)2+y2]=a4,对4个选项加以验证,即可得出结论.
解答 解:由题意设P(x,y),则$\sqrt{(x+c)^{2}+{y}^{2}}•\sqrt{(x-c)^{2}+{y}^{2}}$=a2,
即[(x+c)2+y2]•[(x-c)2+y2]=a4,
①当a=0,c=1时,轨迹为两个点F1(-1,0),F2(1,0),正确;
②a=c,(0,0)代入,方程成立则曲线过原点,即故②正确;
③∵(|PF1|+|PF2|)min=2c,(当且仅当,|PF1|=|PF2|=c时取等号),
∴(|PF1||PF2|)min=c2,
∴若0<a<c,则曲线不存在,故③正确;
④把方程中的x被-x代换,方程不变,故此曲线关于y轴对称;
把方程中的y被-y 代换,方程不变,故此曲线关于x轴对称;
把方程中的x被-x代换,y被-y 代换,方程不变,
故此曲线关于原点对称;故④正确;
故答案为:①②③④.
点评 本题考查新定义,考查学生分析解决问题的能力,正确运用新定义是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow{a}$=$\overrightarrow{b}$,$\overrightarrow{b}$=$\overrightarrow{c}$,则$\overrightarrow{a}$=$\overrightarrow{c}$ | B. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C. | 若λ$\overrightarrow{a}$=0(λ为实数),则λ=0 | D. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{b}$∥$\overrightarrow{c}$,则$\overrightarrow{a}$∥$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
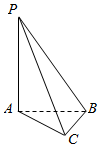 如图,在四面体P-ABC中,PA、AB、BC两两垂直,且AB=$\sqrt{6}$,BC=$\sqrt{2}$,则二面角B-AP-C的大小为( )
如图,在四面体P-ABC中,PA、AB、BC两两垂直,且AB=$\sqrt{6}$,BC=$\sqrt{2}$,则二面角B-AP-C的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\overrightarrow{DA}$ | B. | 2$\overrightarrow{AD}$ | C. | 2$\overrightarrow{BD}$ | D. | 2$\overrightarrow{DB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,△ABC是边长为2的正三角形,BC∥平面α,且A、B、C在平面α的同侧,它们在α内的正射影分别是A′、B′、C′,且△A′B′C′是Rt△,BC到α的距离为5.
如图所示,△ABC是边长为2的正三角形,BC∥平面α,且A、B、C在平面α的同侧,它们在α内的正射影分别是A′、B′、C′,且△A′B′C′是Rt△,BC到α的距离为5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com