练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．一只蚂蚁在高为3，两底分别为3和7的直角梯形区域内随机爬行，则其恰在离四个顶点距离都大于1的地方的概率为$\frac{15-π}{15}$．

    分析 以四个顶点为圆心，1为半径作圆，当蚂蚁在此区域外的区域随机爬行，离顶点的距离大于1，其面积为15-π，再用几何概型公式即得本题的概率

    解答 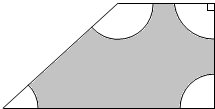解：如图由已知，高为3，两底分别为3和7的直角梯形面积为$\frac{1}{2}$×3×（3+7）=15，
    离四个顶点距离都大于1的区域是如图阴影部分，即以四个顶点为圆心，1为半径作圆，当蚂蚁在除此区域外的区域随机爬行，离顶点的距离大于1的部分，其面积为=15-π，
    ∴蚂蚁恰在离四个顶点距离都大于1的地方的概率为P=$\frac{15-π}{15}$．
    故答案为：$\frac{15-π}{15}$．

    点评 本题几何概型的概率．着重考查了图形面积的求法和几何概型的概率求法等知识点，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知命题P：?x∈R，x2+2x+2＜0，则￢P为（　　）
    A．?x∈R，x2+2x+2≥0，真命题B．?x∈R，x2+2x+2＜0，假命题
    C．?x∉R，x2+2x+2≥0，假命题D．?x∈R，x2+2x+2≥0，真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．数列{an}满足a1=1，且an+1-an=n+1（n∈N+），则数列$\left\{{\frac{1}{a_n}}\right\}$的前10项和为（　　）
    A．$\frac{2}{5}$B．$\frac{20}{11}$C．$\frac{11}{20}$D．$\frac{5}{7}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．函数y=2sinx（-π≤x≤π）的大致图象为（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=loga（1+x），g（x）=loga（1-x）其中（a＞0且a≠1），设h（x）=f（x）-g（x）
    （Ⅰ）求函数h（x）的定义域，判断h（x）的奇偶性，并说明理由．
    （Ⅱ）若f（3）=2，求使h（x）＜0成立的x的集合．
    （Ⅲ）若a＞1，当$x∈[0，\frac{1}{2}]$时，h（x）∈[0，1]，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

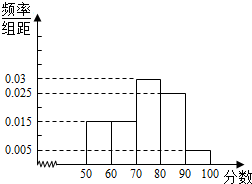    20．为更好地迎接江苏省学业水平测试，某校针对本届高二文科学生，进行了物理学科模拟测试，从参加测试的学生中抽出60名学生，对他们的物理成绩进行统计（注：学生成绩均为整数且满分为100分），并把其中成绩不低于50分的分成五段：[50，60），[60，70）…[90，100]，画出如下部分频率分布直方图．请观察图形的相关信息，回答下列问题：
    （1）根据江苏省高中学业水平测试要求，成绩低于60分的属于不合格需要补考，求抽取的60名学生中需要补考的学生人数；
    （2）根据江苏省高中学业水平测试要求，成绩为60分或高于60分的属于合格，成绩为90分或高于90分的属于优秀，估计本次测试物理学科的合格率和优秀率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．求函数y=$\sqrt{3}$cos2x-sinxcosx+3的最大值、最小值和周期．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．不等式组$\left\{\begin{array}{l}{3x-1＞7}\\{5-8x＜4x-1}\end{array}\right.$的解集用区间表示为（$\frac{8}{3}$，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知在锐角△ABC中，∠B=45°，b=10，c=5$\sqrt{6}$，求△ABC的面积．

    查看答案和解析>>

    同步练习册答案