
(本小题满分13分)
设a、b、c分别是先后掷一枚质地均匀的正方体骰子三次得到的点数.
(1)求使函数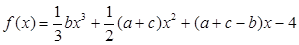 在R上不存在极值点的概率;
在R上不存在极值点的概率;
(2)设随机变量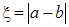 ,求
,求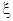 的分布列和数学期望.
的分布列和数学期望.
(1)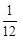 (2)
(2)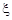 的分布列为
的分布列为
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
|
|
|
|
|
|
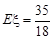
【解析】
试题分析:(1) ………………………………………(1分)
………………………………………(1分)
若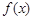 在R上不存在极值点,则
在R上不存在极值点,则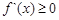 恒成立
恒成立
∴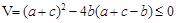 …………………………………………………………(2分)
…………………………………………………………(2分)
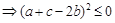
∴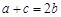
又a,b,c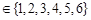
∴a、b、c成等差数列……………………………………………………………………(4分)
按公差分类,a、b、c成等差数列共有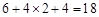 种情况
种情况
故函数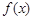 在R上不存在极值点的概率
在R上不存在极值点的概率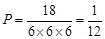 ……………………………(6分)
……………………………(6分)
(2)若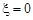 ,则
,则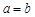 ∴
∴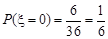
若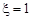 ,则
,则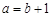 或
或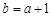 ,
,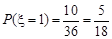
同理: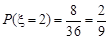
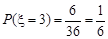
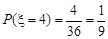
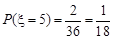 ……………………………………(10分)
……………………………………(10分)
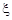 的分布列为
的分布列为
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
|
|
|
|
|
|
∴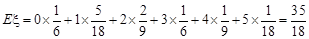 ………………………………(13分)
………………………………(13分)
考点:函数极值古典概率及分布列期望
点评:函数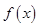 无极值点则导数
无极值点则导数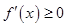 或
或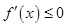 恒成立;古典概型概率需找到所有的基本事件总数及满足题目要求的基本事件种数,求其比值;分布列首先找到随机变量可取的值,然后结合题目背景依次求出各个概率
恒成立;古典概型概率需找到所有的基本事件总数及满足题目要求的基本事件种数,求其比值;分布列首先找到随机变量可取的值,然后结合题目背景依次求出各个概率


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源:2015届江西省高一第二次月考数学试卷(解析版) 题型:解答题
(本小题满分13分)已知函数
 .
.
(1)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(2)在给出的直角坐标系中,画出函数 在区间
在区间 上的图象.
上的图象.
(3)设0<x< ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三年级八月份月考试卷理科数学 题型:解答题
(本小题满分13分)已知定义域为 的函数
的函数 是奇函数.
是奇函数.
(1)求 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性;
(3)若对任意的 ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源:河南省09-10学年高二下学期期末数学试题(理科) 题型:解答题
(本小题满分13分)如图,正三棱柱 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求异面直线 与
与 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

[来源:KS5
U.COM
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三5月月考调理科数学 题型:解答题
(本小题满分13分)
已知 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
.
(1) 求函数 的表达式;
的表达式;
(2)在 中,若
中,若 A=2
A=2 ,
, ,BC=2,求
,BC=2,求 的面积
的面积
(3) 求数列 的前
的前 项和
项和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com