
| 1 |
| 2 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 20 |
| 81 |
| 5 |
| 9 |
| 5 |
| 9 |
| 16 |
| 81 |
| 5 |
| 9 |
| 20 |
| 81 |
| 16 |
| 81 |
| 266 |
| 81 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014届安徽省高三第一次月考理科数学试卷(解析版) 题型:解答题
甲、乙两人进行围棋比赛,规定每局胜者得1分,负者得0分,比赛进行到有一方比对方多2分或打满6局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
.
(Ⅰ)求 的值;
的值;
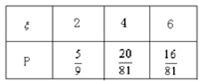
(Ⅱ)设 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
查看答案和解析>>
科目:高中数学 来源:0127 模拟题 题型:解答题
 ),且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为 。
。查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都外国语学校高三(上)10月月考数学试卷(解析版) 题型:解答题
 ),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省师大附中等重点学校高三联考数学试卷(理科)(解析版) 题型:解答题
 ),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com