
| A. | (1,2) | B. | (2,1+$\sqrt{2}$) | C. | ($\frac{1}{2}$,1) | D. | (1+$\sqrt{2}$,+∞) |
分析 根据双曲线的对称性,得到等腰△ABE中,∠AEB为锐角,可得|AF|<|EF|,将此式转化为关于a、c的不等式,化简整理即可得到该双曲线的离心率e的取值范围.
解答 解:根据双曲线的对称性,得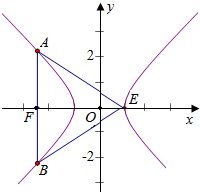
△ABE中,|AE|=|BE|,
△ABE是锐角三角形,即∠AEB为锐角,
由此可得Rt△AFE中,∠AEF<45°,
得|AF|<|EF|
∵|AF|=$\frac{{b}^{2}}{a}$=$\frac{{c}^{2}-{a}^{2}}{a}$,|EF|=a+c,
∴$\frac{{c}^{2}-{a}^{2}}{a}$<a+c,即2a2+ac-c2>0,
两边都除以a2,得e2-e-2<0,解之得-1<e<2,
∵双曲线的离心率e>1,
∴该双曲线的离心率e的取值范围是(1,2)
故选:A.
点评 本题给出双曲线过一个焦点的通径与另一个顶点构成锐角三角形,求双曲线离心率的范围,着重考查了双曲线的标准方程与简单几何性质等知识,属于中档题.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①和③ | B. | ①和② | C. | ①和④ | D. | ③和④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 奖品 收费(元/件) 工厂 | 一等奖奖品 | 二等奖奖品 |
| 甲 | 500 | 400 |
| 乙 | 800 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<1} | B. | {x|x<-2或x≥3} | C. | {x|-2<x≤1} | D. | {x|-2<x<3且x≠1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
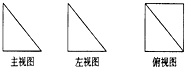 如图,是一个空间几何体的主视图(正视图)、左视图、俯视图,如果图中直角三角形的直角边长均为1,那么这个几何体的侧面积为( )
如图,是一个空间几何体的主视图(正视图)、左视图、俯视图,如果图中直角三角形的直角边长均为1,那么这个几何体的侧面积为( )| A. | 1+$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 1+2$\sqrt{2}$ | D. | 2+2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com